题目内容
如图甲所示,两平行金属板长度l=0.2m,两板间电压U随时间t变化的图象如图乙所示.在金属板右侧有一左边界为MN的匀强磁场,磁感应强度B=0.01T,方向垂直纸面向里.现有带正电的粒子连续不断地以速度v0=105m/s射入电场中,初速度方向沿两板间的中线OO′方向.磁场边界MN与中线OO′垂直.已知带电粒子的比荷q/m=108C/kg,粒子的重力和粒子之间的相互作用力均可忽略不计.
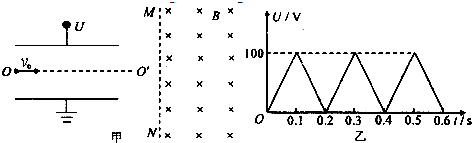
(1)在每个粒子通过电场区域的时间内,可以把板间的电场强度看作是恒定的.请通过计算说明这种处理的合理性;
(2)设t=0.1s时刻射入电场的带电粒子恰能从金属板边缘穿越电场射入磁场,求该带电粒子射出电场时速度的大小;
(3)对于所有经过电场射入磁场的带电粒子,设其射入磁场的入射点和从磁场射出的出射点间的距离为d,试通过推理判断d的大小是否随时间变化?
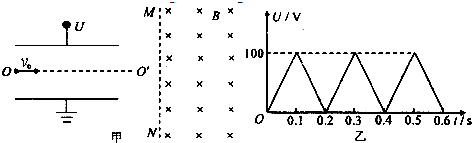
(1)在每个粒子通过电场区域的时间内,可以把板间的电场强度看作是恒定的.请通过计算说明这种处理的合理性;
(2)设t=0.1s时刻射入电场的带电粒子恰能从金属板边缘穿越电场射入磁场,求该带电粒子射出电场时速度的大小;
(3)对于所有经过电场射入磁场的带电粒子,设其射入磁场的入射点和从磁场射出的出射点间的距离为d,试通过推理判断d的大小是否随时间变化?
分析:(1)粒子在垂直电场方向做匀速直线运动,求出粒子在电场中的运动时间,与电压变化的周期比较确定电场强度能视为恒定.
(2)根据偏转的电压得出出射点和入射点间的电压,根据动能定理求出粒子射出电场时的速度大小.
(3)抓住粒子在垂直电场方向上的速度不变,根据平行四边形定则求出粒子进入磁场时的速度,通过半径公式和几何关系求出进入磁场的入射点和出射点的距离,从而进行判断.
(2)根据偏转的电压得出出射点和入射点间的电压,根据动能定理求出粒子射出电场时的速度大小.
(3)抓住粒子在垂直电场方向上的速度不变,根据平行四边形定则求出粒子进入磁场时的速度,通过半径公式和几何关系求出进入磁场的入射点和出射点的距离,从而进行判断.
解答:解:(1)带电粒子在金属板间运动的时间为
t=
=
s=2×10-6s
电压U变化周期 T=0.2s;
由于t远小于T,故在粒子通过电场的时间内板间电压变化极小,板间电场可视为恒定不变.
(2)t=0.1s时刻偏转电压 U=100V
由动能定理得:
qU=
m
-
m
解得:v1=1.41×105m/s
(3)设某时刻射出电场的粒子速度为v,速度方向与OO′夹角为θ,则
v=
粒子在磁场中有 qvB=
由几何关系得:d=2Rcosθ
由以上各式解得:d=
=0.2m
显然d不随时间变化.
答:
(1)在每个粒子通过电场区域的时间内,可以把板间的电场强度看作是恒定的.计算说明见上;
(2)该带电粒子射出电场时速度的大小为1.41×105m/s;
(3)d不随时间变化.
t=
| l |
| v0 |
| 0.2 |
| 105 |
电压U变化周期 T=0.2s;
由于t远小于T,故在粒子通过电场的时间内板间电压变化极小,板间电场可视为恒定不变.
(2)t=0.1s时刻偏转电压 U=100V
由动能定理得:
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 0 |
解得:v1=1.41×105m/s
(3)设某时刻射出电场的粒子速度为v,速度方向与OO′夹角为θ,则
v=
| v0 |
| cosθ |
粒子在磁场中有 qvB=
| mv2 |
| R |
由几何关系得:d=2Rcosθ
由以上各式解得:d=
| 2mv0 |
| qB |
显然d不随时间变化.
答:
(1)在每个粒子通过电场区域的时间内,可以把板间的电场强度看作是恒定的.计算说明见上;
(2)该带电粒子射出电场时速度的大小为1.41×105m/s;
(3)d不随时间变化.
点评:本题考查带电粒子在电场中的偏转和在磁场中做圆周运动,掌握在电场中运动时在沿电场方向和垂直磁场方向上的运动规律,以及掌握在磁场中运动的半径公式,结合几何关系进行求解.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
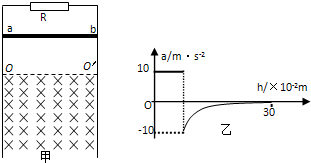 (2011?徐州一模)如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
(2011?徐州一模)如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:

 如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求: =1x108C/kg、初速度v0=2x 105m/s的带正电粒子.忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极 板间的电压变化.sin30=0.5,sin37=0.6,sin45=
=1x108C/kg、初速度v0=2x 105m/s的带正电粒子.忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极 板间的电压变化.sin30=0.5,sin37=0.6,sin45= .
.