题目内容
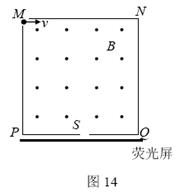
（17分）从粒子源不断发射相同的带电粒子，初速可忽略不计，这些粒子经电场加速后，从M孔以平行于MN方向进入一个边长为d的正方形的磁场区域MNQP，如图14所示，磁感应强度大小为B，方向垂直纸面向外，其中PQ的中点S开有小孔，外侧紧贴PQ放置一块荧光屏。当把加速电压调节为U时，这些粒子刚好经过孔S 打在荧光屏上，不计粒子的重力和粒子间的相互作用。请说明粒子的电性并求出粒子的比荷（
）
解：粒子在磁场中运动轨迹如答图2所示，
其中O为轨迹的圆心。由于受力沿MP边，粒子带正电。（2分）
粒子在电场中加速，由动能定理有：
解得：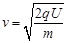
①（3分）
粒子进入磁场中做圆周运动，由洛伦兹力提供向心力得：
解得
②（3分）
又由轨迹图，在ΔOSP中有：
解得
③（5分）
将③与①式代入②解得：
。（4分）
解析:应用动能定理求出带电粒子经电场加速后的速度，画出带电粒子在磁场中运动轨迹图，利用洛伦兹力提供向心力和图中几何关系列方程解答。
练习册系列答案
相关题目
如图所示，在x＞0，y＞0的空间存在沿y轴负方向的匀强电场，场强大小为E．一粒子源不断地发射相同的带电粒子，粒子的初速度恒定，当粒子从（0，a）处沿x轴正方向射入匀强电场后恰好从（b，0）处射出．撤去电场在此区域加一方向垂直于xOy平面的匀强磁场，磁感应强度为B，其他条件不变，粒子仍恰好从（b，0）处射出．已知Oa=3L，Ob=
）
）。
）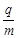