题目内容
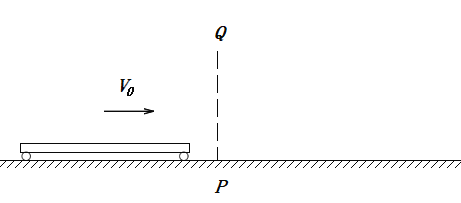
【题目】如图所示，水平面上有一条长直固定轨道，P为轨道上的一个标记点，竖直线PQ表示一个与长直轨道垂直的竖直平面，PQ的右边区域内可根据需要增加一个方向与轨道平行的水平匀强电场。在轨道上，一辆平板小车以速度v=4m/s沿轨道从左向右匀速运动，当车长一半通过PQ平面时，一质量为m=1kg的绝缘金属小滑块（可视为质点）被轻放到小车的中点上，已知小滑块带电荷量为+2C且始终不变，滑块与小车上表面间的动摩擦因数为μ=0.2，整个过程中小车速度保持不变，g=10m/s2，求：
(1)若PQ右侧没有电场，小车足够长，在滑块与小车恰好共速时小滑块相对P点水平位移和摩擦力对小车做的功；
(2)若PQ右侧加一个向右的匀强电场，且小车长L=2m，为确保小滑块不从小车左端掉下来，电场强度大小应满足什么条件？
(3)在（2）的情况下，PQ右侧电场强度取最小值时，为保证小滑块不从车上掉下，则电场存在的时间满足什么条件？
【答案】(1)4m，－16J(2)
(3)
【解析】
(1)小滑块放上小车后向右做匀加速运动，根据牛顿第二定律得
解得
设加速到共速时用时为t1，则
，解得
此过程中小滑块相对于P点移动的距离为
，此过程中小车相对于P点移动的距离为
，可得
摩擦力对小车做的功
解得
(2)当加有向右的匀强电场时，小滑块的加速度为
小滑块恰好运动到小车左端共速，用时
，根据两物体的位移关系可得
联立解得
所以电场强度E应满足E≥3V/m；
(3)满足第二问的条件，当E=3V/m时，小滑块运动到小车最左端后，会向右做匀加速运动，设时间为t3后撤去电场，之后滑块做减速运动，经过时间t4，小滑块与小车在小车右端共速，恰好没掉下来。小滑块向右加速时有
解得
加速的末速度为
，减速过程中
，加速过程中的位移为
减速过程中的位移为
则
解得
所以，电场存在总时间
故电场存在的时间满足关系式
