题目内容
【题目】如图所示,空间同时存在相互垂直的匀强磁场和匀强电场,磁场垂直纸面向里,磁感应强度B=2.0T;电场方向和竖直方向夹角α=60°。一个带正电的微粒从空间的S点出发,沿SP方向以v=4m/s的速度做匀速直线运动,运动方向与竖直方向夹角θ=30°,微粒运动一段时间后,电场方向变为竖直向上,场强E大小不变,微粒立即做圆周运动,其圆心在过S点的竖直线上,某时刻磁场又突然消失(电场仍然竖直向上),微粒最终恰能回到S点,重力加速度![]() ,求
,求

(1)匀强电场的场强大小;
(2)微粒做匀速直线运动的时间(结果可用根式表示)。
【答案】(1)8.0N/C(2)![]()
【解析】(1)微粒沿SP方向做直线运动过程中,受重力mg、电场力qE和洛伦兹力qvB,该运动为匀速直线运动,则三力合力Wie零,如图1所示
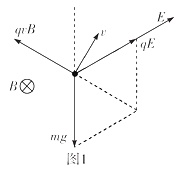
由于三力平衡且互成120°,由几何关系可知三力等大
则qE=mg,qvB=mg
解得![]()
(2)电场变为竖直向上后,电场力与重力平衡,微粒在洛伦兹力作用下做匀速圆周运动,有![]()
解得![]()
画出微粒运动的轨迹如图2所示
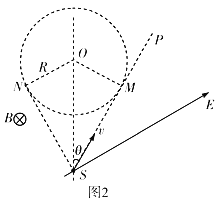
由轨迹可知,微粒在M点开始做圆周运动,在N点磁场消失,微粒又做匀速直线运动回到S点,根据几何关系可得![]() ,即
,即![]()
微粒做匀速直线运动的时间![]()

练习册系列答案
相关题目