题目内容
【题目】如图所示,粗糙水平地面AB与半径R=0.4m的光滑半圆轨道BCD相连接,且在同一竖直平面内,O是BCD的圆心,BOD在同一竖直线上.质量m=2kg的小物体在9N的水平恒力F的作用下,从A点由静止开始做匀加速直线运动.已知AB=5m,小物块与水平地面间的动摩擦因数为μ=0.2.当小物块运动到B点时撤去力F.取重力加速度g=10m/s2.求:
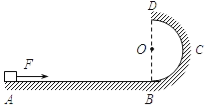
(1)小物块到达B点时速度的大小;
(2)小物块运动到D点时的速度;
(3)小物块离开D点落到水平地面上的点与B点之间的距离.
【答案】(1)小物块到达B点时速度的大小是5m/s
(2)小物块运动到D点时的速度是3m/s
(3)小物块离开D点落到水平地面上的点与B点之间的距离是1.2m
【解析】
试题分析:(1)从A到B,根据动能定理有:
(F﹣μmg)x=![]()
代入数据得:vB=5m/s
(2)从B到D,根据机械能守恒定律有:
![]() =
=![]() +mg2R
+mg2R
代入数据解得:vD=3m/s
(3)由D点到落点小物块做平抛运动,在竖直方向有
2R=![]()
得 t=2![]() =2×
=2×![]() =0.4s
=0.4s
水平面上落点与B点之间的距离为:x=vDt=3×0.4=1.2m

练习册系列答案
相关题目