题目内容
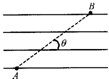一个带正电的微粒，从A点射入水平方向的匀强电场中，微粒沿直线AB运动，如图，AB与电场线夹角θ=30°，已知带电微粒的质量m=1.0×10-7kg，电量q=1.0×10-10C，A、B相距L=20cm．（取g=10m/s2，结果保留二位有效数字）求：（1）说明微粒在电场中运动的性质．
（2）电场强度的大小和方向？
（3）要使微粒到达B点时的速度恰好为0，微粒射入电场时的速度是多少？
分析：（1）带电微粒做直线运动，可判断出电场力的方向，根据合力情况确定出微粒在电场中运动的性质．
（2）微粒做直线运动时，合力与速度在同一直线上，由力的合成，求出电场强度的大小和方向；
（3）微粒从A点运动到B点，做匀减速运动，刚好到B点速度为零，由运动学公式求解微粒射入电场时的最小速度．
（2）微粒做直线运动时，合力与速度在同一直线上，由力的合成，求出电场强度的大小和方向；
（3）微粒从A点运动到B点，做匀减速运动，刚好到B点速度为零，由运动学公式求解微粒射入电场时的最小速度．
解答：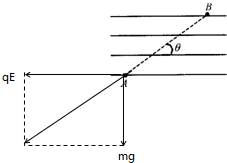
解：（1）带电微粒在电场中受到电场力qE和重力mg，电场力水平向右或方向向左，由于带电微粒沿直线AB运动，可判断出电场力的方向水平向左，则电场力、重力的合力与速度相反，微粒做匀减速在线运动．
加速度大小为a=
=
=20m/s2．
故微粒做加速度大小为20m/s2的匀减速直线运动；
（2）由qE=mgcot30°
得：E=
=1.7×104N/C，方向向左；
（3）微粒从A点运动到B点，做匀减速运动，刚好到B点速度为零，由0-
=-2aL得，
v0=
代入解得，v0=2.8m/s；
答：（1）微粒在电场中运动的性质是：微粒做加速度大小为20m/s2的匀减速直线运动；
（2）电场强度的大小为1.7×104N/C，方向向左；
（3）要使微粒从A点运动到B点，微粒射入电场时的最小速度是2.8m/s．
解：（1）带电微粒在电场中受到电场力qE和重力mg，电场力水平向右或方向向左，由于带电微粒沿直线AB运动，可判断出电场力的方向水平向左，则电场力、重力的合力与速度相反，微粒做匀减速在线运动．加速度大小为a=
| F 合 |
| m |
| ||
| m |
故微粒做加速度大小为20m/s2的匀减速直线运动；
（2）由qE=mgcot30°
得：E=
| mgcot30° |
| q |
（3）微粒从A点运动到B点，做匀减速运动，刚好到B点速度为零，由0-
| v | 2 0 |
v0=
| 2aL |
答：（1）微粒在电场中运动的性质是：微粒做加速度大小为20m/s2的匀减速直线运动；
（2）电场强度的大小为1.7×104N/C，方向向左；
（3）要使微粒从A点运动到B点，微粒射入电场时的最小速度是2.8m/s．
点评：本题要掌握质点做直线运动的条件：合力与速度共线，由牛顿第二定律和运动学公式结合进行研究．
练习册系列答案
阅读快车系列答案
相关题目
一个带正电的微粒，从A点射入水平方向的匀强电场中，微粒沿直线AB运动，如图，AB与电场线夹角θ=30°，已知带电微粒的质量m=1.0×10-7kg，电量q=1.0×10-10C，A、B相距L=20cm．（取g=10m/s2，结果保留二位有效数字）求：
一个带正电的微粒，从A点射入水平方向的匀强电场中，微粒沿直线AB运动，如图所示，AB与电场线夹角θ=30°．已知带电微粒的质量m=1.0×10-7kg，电量q=1.0×10-10C，A、B相距L=20cm．（取g=10m/s2，结果要求二位有效数字）求：
一个带正电的微粒，从A点射入水平方向的匀强电场中，微粒沿直线由A向B运动，如图所示，AB与电场线夹角为θ．已知带电微粒的质量为m，电荷量为q，A、B相距L（重力加速度为g）．
一个带正电的微粒，从A点射入水平方向的匀强电场中，微粒沿直线AB运动，AB与电场线夹角θ．已知带电微粒的质量m，电量q，A、B相距L．则以下说法不正确的是（ ）