题目内容
6. 如图所示,一质量为m的带电+q的小球初速度v0与水平方向成30°角.
如图所示,一质量为m的带电+q的小球初速度v0与水平方向成30°角.①若保证小球做匀速直线运动,施加一个怎样的电场?
②若保证小球做匀加速直线运动,施加一个与水平方向成60°角的电场,则E=?
③若保证小球做匀减速直线运动,施加一个场强最小的电场,则E=?
④若保证小球做类平抛运动,施加一个场强最小的电场,则E=?
⑤若保证小球做匀速圆周运动,(此情形不计小球重力),施加一个怎样的电场?
分析 ①对小球进行受力分析,小球受到的合外力为0时做匀速直线运动;
②对小球进行受力分析,小球受到与初速度方向相同的合外力时,小球做匀加速直线运动;
③对小球进行受力分析,小球受到与初速度方向相反的合外力时,小球做匀减速直线运动;
④对小球进行受力分析,小球受到的合外力的方向与初速度的方向垂直时,小球做类平抛运动;
⑤对小球进行受力分析,小球受到大小不变,方向不断变化,而且恰好等于需要的向心力的合外力时,小球做匀速圆周运动.
解答 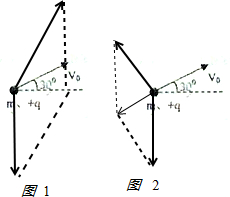 解:①小球受到重力与电场力的作用,当小球受到的合外力为0时做匀速直线运动,所以电场力qE=mg,电场力的方向与重力的方向相反,所以需要加一个方向竖直向上、大小是$\frac{mg}{q}$的电场.
解:①小球受到重力与电场力的作用,当小球受到的合外力为0时做匀速直线运动,所以电场力qE=mg,电场力的方向与重力的方向相反,所以需要加一个方向竖直向上、大小是$\frac{mg}{q}$的电场.
②当小球受到与初速度方向相同的合外力时,小球的受力如图1,
竖直方向:qEsin60°-mg=ma•sin30°
水平方向:qEcos60°=ma•cos30°
联立得:E=$\frac{\sqrt{3}mg}{q}$
③小球受到与初速度方向相反的合外力时,小球做匀减速直线运动当电场力的方向与合力的方向垂直时,电场力最小,场强最小,如图2,则:qE=mgsin60°
所以:$E=\frac{\sqrt{3}mg}{2q}$
④小球做类平抛运动,则合力的方向与初速度的方向垂直,当电场力的方向与合力的方向垂直时,电场力最小,场强最小,此时:
qE=mgsin30°
得:$E=\frac{mg}{2q}$
⑤若保证小球做匀速圆周运动,则在重力不计的条件下,则电场力提供向心力,此时:$qE=\frac{m{v}_{0}^{2}}{r}$
由于向心力的大小不变而方向始终与速度的方向垂直,所以需要加一个点电荷的电场,该点电荷的位置在与初速度垂直的方向上,同时要满足:
$\frac{kQq}{{r}^{2}}=\frac{m{v}_{0}^{2}}{r}$
答:①若保证小球做匀速直线运动,施加一个方向竖直向上、大小是$\frac{mg}{q}$的电场.
②若保证小球做匀加速直线运动,施加一个与水平方向成60°角的电场,则E=$\frac{\sqrt{3}mg}{q}$;
③若保证小球做匀减速直线运动,施加一个场强最小的电场,则$E=\frac{\sqrt{3}mg}{2q}$;
④若保证小球做类平抛运动,施加一个场强最小的电场,则$E=\frac{mg}{2q}$;
⑤若保证小球做匀速圆周运动,(此情形不计小球重力),需要加一个点电荷的电场,该点电荷的位置在与初速度垂直的方向上,同时要满足:$\frac{kQq}{{r}^{2}}=\frac{m{v}_{0}^{2}}{r}$.
点评 该题考查带电粒子在电场中的运动,解答本题关键要掌握小球做直线运动的条件:合力方向与速度方向共线,运用作图法得到电场力的最小值.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案| A. | 质点某一秒末的速度一定比前一秒末的速度大2a | |
| B. | 质点某一秒末的速度一定比前一秒初的速度大2a | |
| C. | 若a是变值,在a减小到零的过程中,速度的变化减小到零,末速度仍为V0 | |
| D. | 若a是变值,在a减小到零后,物体运动最快 |
 如图,以直角三角形AOC为边界的有界匀强磁场区域,磁场方向垂直于纸面向里,磁感应强度大小为B,∠A=60°,AO=a.在O点放置一个粒子源,可以向纸面内各个方向发射某种带负电粒子,粒子的比荷为$\frac{q}{m}$,速度大小都为v0,且满足v0=$\frac{qBa}{m}$,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法不正确的是( )
如图,以直角三角形AOC为边界的有界匀强磁场区域,磁场方向垂直于纸面向里,磁感应强度大小为B,∠A=60°,AO=a.在O点放置一个粒子源,可以向纸面内各个方向发射某种带负电粒子,粒子的比荷为$\frac{q}{m}$,速度大小都为v0,且满足v0=$\frac{qBa}{m}$,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法不正确的是( )| A. | 粒子在磁场中运动的半径为a | |
| B. | 粒子有可能打到A点 | |
| C. | 以θ=60°飞入的粒子在磁场中运动时间最短 | |
| D. | 在AC边界上只有一半区域有粒子射出 |
| A. | F一定大于任何一个分力 | |
| B. | F的大小可能等于F1,也可能等于F2 | |
| C. | 若把F分解,若知道两个分力的方向(与合力不共线),则只能作出唯一一个平行四边形 | |
| D. | F的大小随F1、F2间的夹角的增大而减小 |
 如图所示,将长0.20m的直导线全部放入匀强磁场中,保持导线和磁场方向垂直.当导线中通过的电流为2.0A时,该直导线受到安培力的大小是2.0×10-3N,则此匀强磁场的磁感应强度的大小为( )
如图所示,将长0.20m的直导线全部放入匀强磁场中,保持导线和磁场方向垂直.当导线中通过的电流为2.0A时,该直导线受到安培力的大小是2.0×10-3N,则此匀强磁场的磁感应强度的大小为( )| A. | 5.0×10-3T | B. | 8.0×10-4T | C. | 2.0×10-3T | D. | 1.0×10-4T |
 如图,两光滑的金属导轨之间存在一匀强磁场,方向垂直指向纸里.导轨的一端经导线与一灯泡A相接,另一端用导线闭合,一金属框置于导轨之上,框与灯泡B串联.当金属框按图示方向运动时( )
如图,两光滑的金属导轨之间存在一匀强磁场,方向垂直指向纸里.导轨的一端经导线与一灯泡A相接,另一端用导线闭合,一金属框置于导轨之上,框与灯泡B串联.当金属框按图示方向运动时( )| A. | A、B两盏灯都不亮 | B. | A、B两盏灯都发亮 | C. | 灯泡A发亮,B不亮 | D. | 灯泡A不亮,B发亮 |
| A. | 布朗运动是液体分子的热运动 | |
| B. | 布朗运动反映了液体分子的热运动 | |
| C. | 两个分子间距离小于r0时,分子间只有斥力 | |
| D. | 分子间的引力和斥力同时存在 | |
| E. | 气体总是很容易充满容器,这是气体分子间存在斥力的宏观表现 | |
| F. | 光滑的铅块经过挤压后“粘”在一起,这是铅分子间存在引力的宏观表现 |
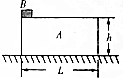 如图,质量为m、长为L、高为h的矩形木块A置于水平地面上,木块与地面间动摩擦因数为μ1,木块上表面光滑,其左端放置一个质量也为m的小物块B.某时刻木块A和小物块B同时获得水平向右的速度v0后开始运动,不计空气阻力,经过一段时间后B落地.
如图,质量为m、长为L、高为h的矩形木块A置于水平地面上,木块与地面间动摩擦因数为μ1,木块上表面光滑,其左端放置一个质量也为m的小物块B.某时刻木块A和小物块B同时获得水平向右的速度v0后开始运动,不计空气阻力,经过一段时间后B落地.