题目内容
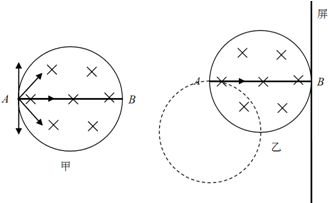
9.一匀强磁场的磁感应强度大小为B,方向垂直于纸面向里,其边界是半径为R的圆,AB为圆的直径.在A点有一粒子源向圆平面内(垂直于磁场)发射质量m、电量-q的粒子,粒子重力不计.(1)如图甲所示,若粒子向圆平面内的各个方向发射,速率均为v1=$\frac{5qBR}{3m}$.求粒子在磁场中运动的最长时间.
(2)如图乙所示,在过B点且垂直于AB方向放置一个很大的屏.若粒子仅沿AB连线方向持续发射,速率均为v2=$\frac{2qBR}{m}$.与此同时,以过A点并垂直于纸面的直线为轴,将磁场顺时针缓慢旋转90°.随着磁场转动,粒子打到屏上的位置会发生变化.求粒子打到屏上的范围.
分析 (1)粒子做匀速圆周运动,速度大小一定,故轨道半径一定,根据牛顿第二定律列式求解轨道半径;当轨迹对应的圆弧最长时,粒子的运动时间最长;
(2)当磁场在实线区域时,画出运动轨迹,得到打在荧光屏上的位置,设为C点;当磁场在虚线区域时,粒子做匀速直线运动,直接打在B点;则BC间距即为粒子打到屏上的范围.
解答 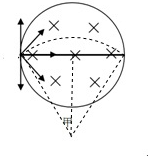 解:(1)粒子做匀速圆周运动,洛仑兹力提供向心力,故:
解:(1)粒子做匀速圆周运动,洛仑兹力提供向心力,故:
$q{v}_{1}B=m\frac{{v}_{1}^{2}}{{r}_{1}}$
解得:${r}_{1}=\frac{m{v}_{1}}{qB}=\frac{5}{3}R$
过直径的弦对应最长时间,如图所示:
结合几何关系,轨迹对应圆心角为:α=2arcsin$\frac{R}{r}$=74°
故运动的最长时间为:tmax=$\frac{74°}{360°}T$=$\frac{74°}{360°}\frac{2πm}{qB}=\frac{37πm}{90qB}$
(2)粒子仅沿AB连线方向持续发射,速率均为v2=$\frac{2qBR}{m}$,洛仑兹力提供向心力,故: $q{v}_{2}B=m\frac{{v}_{2}^{2}}{{r}_{2}}$
$q{v}_{2}B=m\frac{{v}_{2}^{2}}{{r}_{2}}$
解得:${r}_{2}=\frac{m{v}_{2}}{qB}=2R$
画出运动轨迹,如图所示:
θ=arctan$\frac{R}{{r}_{2}}=\frac{1}{2}$=26.6°
故α=2θ=53°
BC=Rtanα=$\frac{4}{3}R$
答:(1)粒子在磁场中运动的最长时间为$\frac{37πm}{90qB}$;
(2)粒子打到屏上的范围为B点下方$\frac{4}{3}R$的区域.
点评 本题关键是明确粒子做圆周运动的向心力来源,根据牛顿第二定律列式求解轨道半径,再结合几何关系列式分析,不难.

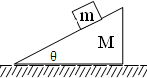
| A. | m沿M上滑时,受到的摩擦力沿斜面向下 | |
| B. | m沿M下滑时,受到的摩擦力沿斜面向上 | |
| C. | m沿斜面滑动时,速度越大,受到的摩擦力越大 | |
| D. | 当斜面倾角增大时,沿斜面滑动的摩擦力将增大 |
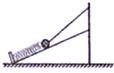 如图,带有竖直支柱的斜面固定在水平地面上,光滑的小球被轻质细线和轻弹簧系住静止于斜面上,弹簧处于拉伸状态.现剪断细线,小球沿斜面向下运动的过程中( )
如图,带有竖直支柱的斜面固定在水平地面上,光滑的小球被轻质细线和轻弹簧系住静止于斜面上,弹簧处于拉伸状态.现剪断细线,小球沿斜面向下运动的过程中( )| A. | 弹簧自然长度前加速运动,之后减速运动 | |
| B. | 弹簧自然长度前加速运动,之后先加速运动后减速运动 | |
| C. | 加速度先增大后减小 | |
| D. | 加速度一直减小 |

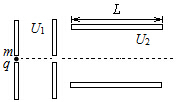 如图所示,质量为m、电量为q的带电粒子静止放入电压为U1的加速电场,然后垂直电场强度方向进入长为L、两极距离为d、电压为U2的偏转电场.求:
如图所示,质量为m、电量为q的带电粒子静止放入电压为U1的加速电场,然后垂直电场强度方向进入长为L、两极距离为d、电压为U2的偏转电场.求: 如图所示,电灯的重力18N,OA绳与顶板间的夹角为37°,OB绳水平,则OA绳所受的拉力F1是30N,OB绳所受的拉力F2是24N.
如图所示,电灯的重力18N,OA绳与顶板间的夹角为37°,OB绳水平,则OA绳所受的拉力F1是30N,OB绳所受的拉力F2是24N. 减速带是交叉路口上常见的一种交通设施,在某小区门口有一橡胶减速带(如图),有一警用巡逻车正以最大速度25m/s从小区门口经过,在离减速带90m时警察发现一逃犯正以10m/s的速度骑电动车匀速通过减速带(电动车始终匀速),而巡逻车要匀减速到5m/s通过减速带(减速带的宽度忽略不计),减速到5m/s后立即以2.5m/s2的加速度加速到最大速度继续追赶,设在整个过程中,巡逻车与逃犯均在水平直道上运动,求从警察发现逃犯到追上逃犯需要的时间.
减速带是交叉路口上常见的一种交通设施,在某小区门口有一橡胶减速带(如图),有一警用巡逻车正以最大速度25m/s从小区门口经过,在离减速带90m时警察发现一逃犯正以10m/s的速度骑电动车匀速通过减速带(电动车始终匀速),而巡逻车要匀减速到5m/s通过减速带(减速带的宽度忽略不计),减速到5m/s后立即以2.5m/s2的加速度加速到最大速度继续追赶,设在整个过程中,巡逻车与逃犯均在水平直道上运动,求从警察发现逃犯到追上逃犯需要的时间.