��Ŀ����
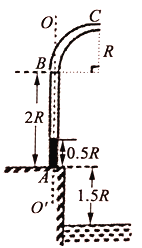
����Ŀ����ͼ��ʾ���⻬ˮƽ��AB����ֱ���ϵİ�Բ�ι̶������B���νӣ�����뾶ΪR��BCΪֱ����һ�ɿ����ʵ㡢����Ϊm�������A�㴦ѹ��һ���ʵ��ɣ�����뵯�ɲ�˩�ӣ����ͷ���飬��鱻���ɵ���������Բ�ι��B��ʱ˲��Թ����ѹ����Ϊ��������7����֮�������˶�ǡ��ͨ����Բ�������ߵ�C���������ٶȴ�СΪg�����ƿ���������������

A. ��龭��B��ʱ���ٶȵĴ�СΪ![]()
B. �տ�ʼʱ��ѹ�����ɵĵ�������Ϊ3mgR
C. ����B�㵽C��˷����������Ĺ�ΪmgR
D. ����ʼʱ��ѹ�����ɵĵ������ܱ�Ϊԭ����2������鵽��C��Ķ���Ϊ![]() mgR
mgR
���𰸡�AB
��������A������龭����Բ���B��˲����ٶ�ΪvB�������B��ʱ���������֧����Ϊ FN=7mg������ţ�ٵڶ�������![]() ���ɵ�
���ɵ�![]() ����A��ȷ��
����A��ȷ��
B������A�㵽B��Ĺ��̣��ɹ��ܹ�ϵ�У��տ�ʼʱ��ѹ�����ɵĵ�������Ϊ Ep==3mgR����B��ȷ��
C������鵽��C��ʱ���ٶ�ΪvC�������C��ʱ��![]() ������B�㵽C��Ĺ��̣��ɶ��ܶ�����
������B�㵽C��Ĺ��̣��ɶ��ܶ�����![]() ���ɽ������B�㵽C����̿˷��������Ĺ� Wf=0.5mgR����C����
���ɽ������B�㵽C����̿˷��������Ĺ� Wf=0.5mgR����C����
D�����տ�ʼʱ��ѹ�����ɵĵ������ܱ�Ϊԭ����2������ʼʱ���ɵĵ�������Ϊ6mgR�����������ڰ�Բ����Ͽ˷�Ħ�����������䣬��ΪWf=0.5mgR���ɹ��ܹ�ϵ�ɵã�6mgR��Wf=2mgR+EKC�����![]() ����ʵ���ϣ����տ�ʼʱ��ѹ�����ɵĵ������ܱ�Ϊԭ����2�����������Բ�ι�����ٶȽ�������ͬһ�����Թ����ѹ����������ܵ��Ļ���Ħ������������B�㵽C��˷�Ħ���������Ĺ���������鵽��C��Ķ���С��
����ʵ���ϣ����տ�ʼʱ��ѹ�����ɵĵ������ܱ�Ϊԭ����2�����������Բ�ι�����ٶȽ�������ͬһ�����Թ����ѹ����������ܵ��Ļ���Ħ������������B�㵽C��˷�Ħ���������Ĺ���������鵽��C��Ķ���С��![]() ����D����
����D����
��ѡ��AB��