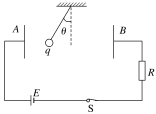
题目内容
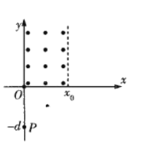
【题目】如图所示，在竖直平面内有一个
坐标系，在
且
区域内有垂直纸面向外的匀强磁场。有一质量为m、带电荷量为+q的小球（可视为质点）从坐标原点O由静止开始自由下落，当小球运动到P（0，-d）点时，在整个空间内突然加一竖直向上的匀强电场（电场强度E的大小未知），使小球从P点返回到O点的时间与从O点下落到P点所用时间相等；当小球返回到O点时，其所带电荷量突然减为原来的
，且再次通过
轴时速度方向与轴正方向间的夹角为30°，已知重力加速度为g，试求：
（1）小球返回O点时的速度大小；
（2）匀强电场的电场强度E的大小和匀强磁场的磁感应强度大小；
（3）小球从O点自由下落到第二次经过轴时的总时间。
【答案】（1）
（2）
；
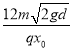（3）
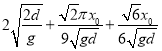
【解析】
（1）设小球从O点运动到P点所用时间为
，在P点的速度为
，返回O点时的速度为
，则有
解得
即
由运动学公式得
解得
（2）小球从O点落到P再返回到O的全过程由动能定理可得
解得
【或用动力学求解为:由牛顿第二定律得
其中
则
当小球返回O点电荷量变为原来的四分之一，根据题意可知，电场力
因此小球将做匀速圆周运动。作粒子运动轨迹如图所示，由几何关系可得
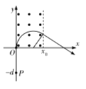
由洛伦兹力提供向心力可得时
解得
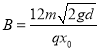
（3）由上可知，小球在磁场中运动时间为
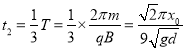
小球离开磁场后做匀速直线运动，由图中几何关系可知
得
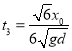
故
.
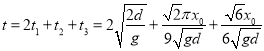练习册系列答案
相关题目
