题目内容
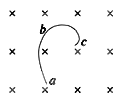
【题目】飞船在离开地球的过程中，经常采用“霍曼变轨”。它的原理很简单：如图所示，飞船先在初始圆轨道Ⅰ上的某一点A打一个脉冲（发动机短暂点火）进行加速，这样飞船就进入一个更大椭圆轨道Ⅱ，其远地点为B。在B点再打一个脉冲进行加速，飞船就进入到最终圆轨道Ⅲ。设轨道Ⅰ为近地轨道，半径为地球半径R,轨道Ⅲ的半径为3R;地球表面重力加速度为g.飞船在轨道Ⅰ的A点的速率为v1，加速度大小为a1;在轨道Ⅱ的A点的速率为v2，加速度大小为a2;在轨道Ⅱ的B点的速率为v3，加速度大小为a3，则（ ）
A. v2>v1>v3
B. a2=a1=g
C. v2=
D. 飞船在轨道Ⅱ上的周期
【答案】ABD
【解析】设飞船在Ⅲ轨道上的速度为
，在地球附近，万有引力提供向心力得
，解得
，由于Ⅲ轨道的半径大，所以
，飞船在Ⅱ轨道经过A点后开始做离心运动，而在I轨道上做匀速圆周运动，根据离心运动条件提供的向心力小于圆周运动所需向心力可得在II轨道上经过A点时的速率大于在I轨道上经过A点时的速率，则
；飞船在Ⅱ轨道经过B点后开始做近心运动，而在Ⅲ轨道上做匀速圆周运动，根据近心运动条件提供的向心力大于圆周运动所需向心力可得在II轨道上经过B点时的速率小于在Ⅲ轨道上经过B点时的速率，则
；比较可得
，A正确；飞船运动过程中由万有引力产生加速度，故在空中同一位置的加速度是相等的；而近地轨道上的加速度等于重力加速度，所以
，B正确；在地球附近，万有引力提供向心力得： 
，解得
，由于
，所以
，C错误；设飞船在近地轨道Ⅰ绕地球运行一周所需的时间为T，则
，卫星在Ⅱ轨道上远地点的距离为3R，近地点的距离为R，则半长轴
；由开普勒第三定律
，所以
，D正确．
练习册系列答案
阅读快车系列答案
相关题目
