题目内容
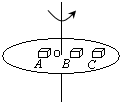 如图,A、B、C三个物体放在匀速旋转圆台上,它们由相同材料制成,A的质量为 2m,B、C的质量各为m,如果OA=OB=R,OC=2R,当圆台旋转时,(设A,B,C都没有滑动).下述结论中正确的是( )
如图,A、B、C三个物体放在匀速旋转圆台上,它们由相同材料制成,A的质量为 2m,B、C的质量各为m,如果OA=OB=R,OC=2R,当圆台旋转时,(设A,B,C都没有滑动).下述结论中正确的是( )分析:三个物体都做匀速圆周运动,角速度相等.根据线速度、向心加速度与角速度的关系分析.对三个物体进行运动分析与受力分析,找出向心力来源,根据向心力公式求出摩擦力,再求出物体受最大静摩擦力时判断哪个物体先滑动.
解答:解:
A、三个物体都没有滑动,都做匀速圆周运动,角速度相等,由v=ωr知,v∝r,则得:物体A、C的线速度之比为1:2;故A正确.
B、向心加速度a=ω2r,ω相等,则a∝r,故物体B、C的向心加速度之比为1:2.故B错误.
C、三个物体所受的合力都指向圆心,对任意一个物体受力分析,如图

根据题意,rC=2rB=2R;
由向心力公式F向=mω2r,得B、C的向心力分别为:
FB=mω2R;
FC=mω2(2R)=2mω2R.
当ω变大时,两个物体所需要的向心力都变大,当达到最大静摩擦力时,物体开始滑动.B所需的向心力与C所需的向心力保持1:2关系.由于B和C受到的最大静摩擦力始终相等,所以C先滑动,B后滑动,故C正确.
D、由于C做匀速圆周运动,由静摩擦力充当向心力,故物体C所受的静摩擦力方向始终指向圆心,与线速度方向始终垂直,故D错误.
故选:AC
A、三个物体都没有滑动,都做匀速圆周运动,角速度相等,由v=ωr知,v∝r,则得:物体A、C的线速度之比为1:2;故A正确.
B、向心加速度a=ω2r,ω相等,则a∝r,故物体B、C的向心加速度之比为1:2.故B错误.
C、三个物体所受的合力都指向圆心,对任意一个物体受力分析,如图

根据题意,rC=2rB=2R;
由向心力公式F向=mω2r,得B、C的向心力分别为:
FB=mω2R;
FC=mω2(2R)=2mω2R.
当ω变大时,两个物体所需要的向心力都变大,当达到最大静摩擦力时,物体开始滑动.B所需的向心力与C所需的向心力保持1:2关系.由于B和C受到的最大静摩擦力始终相等,所以C先滑动,B后滑动,故C正确.
D、由于C做匀速圆周运动,由静摩擦力充当向心力,故物体C所受的静摩擦力方向始终指向圆心,与线速度方向始终垂直,故D错误.
故选:AC
点评:本题关键要抓住三个物体的角速度相等,熟练掌握其他量与角速度的关系,正确分析受力,确定向心力的来源,建立物理模型后分析静摩擦力的方向.

练习册系列答案
相关题目
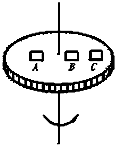 如图,A、B、C三个物体放在水平旋转的圆盘上,三个物体与转盘的最大静摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴距离为R,C离轴2R,若三个物体相对盘静止,则( )
如图,A、B、C三个物体放在水平旋转的圆盘上,三个物体与转盘的最大静摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴距离为R,C离轴2R,若三个物体相对盘静止,则( )| A、每个物体均受重力、支持力、静摩擦力、向心力四个力作用 | B、C的向心加速度最大 | C、B的摩擦力最小 | D、当圆台转速增大时,C比B先滑动,A和B同时滑 |
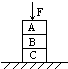 如图,A、B、C三个物体叠放在水平桌面上,在A的上面再施加一个竖直向下的作用力F,则C物体受到竖直向下的作用力除了自身的重力之外还有( )
如图,A、B、C三个物体叠放在水平桌面上,在A的上面再施加一个竖直向下的作用力F,则C物体受到竖直向下的作用力除了自身的重力之外还有( )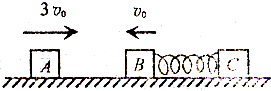 如图,A、B、C三个小木块处于光滑水平面的同一条直线上,质量均为m,B、C分别连接于轻质弹簧两端.现让A以速度3v0向右运动,B、C和处于原长状态的弹簧以速度v0一起向左运动.A与B相碰后迅速粘舍在一起,求此后弹簧的最大弹性势能.
如图,A、B、C三个小木块处于光滑水平面的同一条直线上,质量均为m,B、C分别连接于轻质弹簧两端.现让A以速度3v0向右运动,B、C和处于原长状态的弹簧以速度v0一起向左运动.A与B相碰后迅速粘舍在一起,求此后弹簧的最大弹性势能. 如图,A、B、C三个木块的质量均为m.置于光滑的水平桌面上,B、C之间有一轻质弹簧,弹簧的两端与木块接触而不固连,将弹簧压紧到不能再压缩时用细线把B和C紧连,使弹簧不能伸展,以至于B、C可视为一个整体.现B、C以初速率v0沿B、A的连线方向朝A运动,与A相碰并粘合在一起.以后细线突然断开,弹簧伸展,从而使C与A、B分离.已知C离开弹簧后的速率恰为v0.
如图,A、B、C三个木块的质量均为m.置于光滑的水平桌面上,B、C之间有一轻质弹簧,弹簧的两端与木块接触而不固连,将弹簧压紧到不能再压缩时用细线把B和C紧连,使弹簧不能伸展,以至于B、C可视为一个整体.现B、C以初速率v0沿B、A的连线方向朝A运动,与A相碰并粘合在一起.以后细线突然断开,弹簧伸展,从而使C与A、B分离.已知C离开弹簧后的速率恰为v0.