题目内容
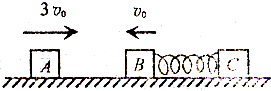 如图,A、B、C三个小木块处于光滑水平面的同一条直线上,质量均为m,B、C分别连接于轻质弹簧两端.现让A以速度3v0向右运动,B、C和处于原长状态的弹簧以速度v0一起向左运动.A与B相碰后迅速粘舍在一起,求此后弹簧的最大弹性势能.
如图,A、B、C三个小木块处于光滑水平面的同一条直线上,质量均为m,B、C分别连接于轻质弹簧两端.现让A以速度3v0向右运动,B、C和处于原长状态的弹簧以速度v0一起向左运动.A与B相碰后迅速粘舍在一起,求此后弹簧的最大弹性势能.分析:A、B碰撞的瞬间,A、B组成的系统动量守恒,根据动量守恒定律求出碰后瞬间AB的速度,当三种速度相同时,弹簧压缩到最短,弹性势能最大,根据动量守恒定律和能量守恒定律求出弹簧的最大弹性势能.
解答:解:A、B碰撞时,C的速度不变,A、B动量守恒,选向右为正方向
m?3v0-mv0=2mv1 ①
A、B一起压缩弹簧,当A、B、C三者速度相等时,弹簧的弹性势能最大,A、B、C和弹簧组成的系统动量和机械能守恒.
2mv1-mv0=3mv2 ②
?2mv12+
mv02=
3mv22+EP ③
由①②③得,弹簧最大弹性势能为EP=
mv02.
答:弹簧最大弹性势能为EP=
mv02.
m?3v0-mv0=2mv1 ①
A、B一起压缩弹簧,当A、B、C三者速度相等时,弹簧的弹性势能最大,A、B、C和弹簧组成的系统动量和机械能守恒.
2mv1-mv0=3mv2 ②
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由①②③得,弹簧最大弹性势能为EP=
| 4 |
| 3 |
答:弹簧最大弹性势能为EP=
| 4 |
| 3 |
点评:本题综合考查了动量守恒定律和能量守恒定律,综合性较强,对学生的能力要求较高,要加强这方面的训练.

练习册系列答案
相关题目
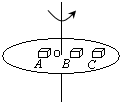 如图,A、B、C三个物体放在匀速旋转圆台上,它们由相同材料制成,A的质量为 2m,B、C的质量各为m,如果OA=OB=R,OC=2R,当圆台旋转时,(设A,B,C都没有滑动).下述结论中正确的是( )
如图,A、B、C三个物体放在匀速旋转圆台上,它们由相同材料制成,A的质量为 2m,B、C的质量各为m,如果OA=OB=R,OC=2R,当圆台旋转时,(设A,B,C都没有滑动).下述结论中正确的是( )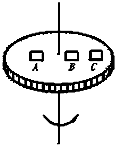 如图,A、B、C三个物体放在水平旋转的圆盘上,三个物体与转盘的最大静摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴距离为R,C离轴2R,若三个物体相对盘静止,则( )
如图,A、B、C三个物体放在水平旋转的圆盘上,三个物体与转盘的最大静摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴距离为R,C离轴2R,若三个物体相对盘静止,则( )| A、每个物体均受重力、支持力、静摩擦力、向心力四个力作用 | B、C的向心加速度最大 | C、B的摩擦力最小 | D、当圆台转速增大时,C比B先滑动,A和B同时滑 |
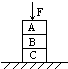 如图,A、B、C三个物体叠放在水平桌面上,在A的上面再施加一个竖直向下的作用力F,则C物体受到竖直向下的作用力除了自身的重力之外还有( )
如图,A、B、C三个物体叠放在水平桌面上,在A的上面再施加一个竖直向下的作用力F,则C物体受到竖直向下的作用力除了自身的重力之外还有( ) 如图,A、B、C三个木块的质量均为m.置于光滑的水平桌面上,B、C之间有一轻质弹簧,弹簧的两端与木块接触而不固连,将弹簧压紧到不能再压缩时用细线把B和C紧连,使弹簧不能伸展,以至于B、C可视为一个整体.现B、C以初速率v0沿B、A的连线方向朝A运动,与A相碰并粘合在一起.以后细线突然断开,弹簧伸展,从而使C与A、B分离.已知C离开弹簧后的速率恰为v0.
如图,A、B、C三个木块的质量均为m.置于光滑的水平桌面上,B、C之间有一轻质弹簧,弹簧的两端与木块接触而不固连,将弹簧压紧到不能再压缩时用细线把B和C紧连,使弹簧不能伸展,以至于B、C可视为一个整体.现B、C以初速率v0沿B、A的连线方向朝A运动,与A相碰并粘合在一起.以后细线突然断开,弹簧伸展,从而使C与A、B分离.已知C离开弹簧后的速率恰为v0.