题目内容
11．
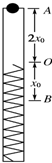如图所示，在一直立的光滑管内放置一轻质弹簧，上端O点与管口A的距离为2x0，一质量为m的小球从管口由静止下落，将弹簧压缩至最低点B，压缩量为x0，不计空气阻力，则（ ）| A． | 当小球与弹簧接触后开始做减速运动 | |
| B． | 小球和弹簧组成的系统在运动过程中机械能守恒 | |
| C． | 弹簧的劲度系数为$\frac{mg}{{x}_{0}}$ | |
| D． | 弹簧的最大弹性势能为3mgx0 |
分析 根据小球的受力，得出加速度的方向，从而判断小球接触弹簧后的运动规律．抓住系统机械能守恒，求出弹簧的最大弹性势能．根据胡克定律求解劲度系数．
解答 解：A、当小球与弹簧接触后，开始重力大于弹力，加速度方向向下，向下做加速运动，然后弹力大于重力，加速度方向向上，向下做减速运动，故A错误．
B、小球和弹簧组成的系统，只有重力和弹簧弹力做功，系统机械能守恒，故B正确．
C、设弹簧的弹力与重力大小相等时，弹簧压缩量为x，则有mg=kx，k=$\frac{mg}{x}$．而弹簧的弹力与重力平衡的位置在B点的上方，则x＜x0，则k＞$\frac{mg}{{x}_{0}}$，故C错误．
D、当小球运动到最低点B时，弹性势能最大，根据机械能守恒定律得，弹簧的最大弹性势能为3mgx0．故D正确．
故选：BD．
点评 本题既要根据受力情况判断小球的运动情况，又要运用机械能守恒分析小球的速度和弹性势能，综合性较强．
练习册系列答案
相关题目
3．以下表述符合物理学史实的是（ ）
| A． | 牛顿通过理想斜面实验发现了物体的运动不需要力来维持 | |
| B． | 伽利略利用实验和推理相结合的方法，得出了力不是维持物体运动的原因 | |
| C． | 伽利略通过观察发现了行星运动的规律 | |
| D． | 牛顿利用扭秤实验，首先测出引力常量，为人类实现飞天梦想奠定了基础 |
如图所示是甲、乙两物体从同一地点开始运动的s-t图线，甲、乙两物体均做匀速直线运动它们运动的方向相同，运动较快的是甲，5s末它们相距10m．
如图所示，倾角为θ=30°、足够长的光滑平行金属导轨MN、PQ相距L1=0.4m，B1=5T的匀强磁场垂直导轨平面向上．一质量m=1.6kg的金属棒ab垂直于MN、PQ放置在导轨上，且始终与导轨接触良好，其电阻r=1Ω．金属导轨上端连接右侧电路，R1=1Ω，R2=1.5Ω．R2两端通过细导线连接质量M=0.6kg的正方形金属框cdef，每根细导线能承受的最大拉力Fm=3.6N，正方形边长L2=0.2m，每条边电阻r0=1Ω，金属框处在一方向垂直纸面向里、B2=3T的匀强磁场中．现将金属棒由静止释放，不计其他电阻及滑轮摩擦，取g=10m/s2．求：
6．2010年诺贝尔物理学奖授予英国曼彻斯特大学科学家安德烈•海姆和康斯坦丁•诺沃肖洛夫，以表彰他们对石墨烯的研究．他们最初是用透明胶带从石墨晶体上“粘”出一片石墨烯的．
我们平常所用的铅笔芯中就含有石墨，能导电．某同学设计了探究铅笔芯伏安特性曲线的实验，得到如下数据（I和U分别表示通过铅笔芯的电流和其两端的电压）：
实验室提供如下器材：
A．电流表A1（量程0.6A，内阻约为1.0Ω）
B．电流表A2（量程3A，内阻约为0.1Ω）
C．电压表V1（量程3V，内阻3kΩ）
D．电压表V2（量程15V，内阻15kΩ）
E．滑动变阻器R1（阻值0～10Ω，额定电流2A）
F．滑动变阻器R2（阻值0～2kΩ，额定电流0.5A）
（1）除长约14cm的中华绘图2B铅笔芯、稳压直流电源E（6V）、开关和带夹子的导线若干外，还需选用的其它器材有ACE（填选项前字母）；
（2）在如图1所示虚线方框中画出实验电路图；
（3）根据表格中数据在图2中画出铅笔芯的I-U图线．
我们平常所用的铅笔芯中就含有石墨，能导电．某同学设计了探究铅笔芯伏安特性曲线的实验，得到如下数据（I和U分别表示通过铅笔芯的电流和其两端的电压）：
| U/V | 0.00 | 0.40 | 0.80 | 1.20 | 1.60 | 2.00 |
| I/A | 0.00 | 0.10 | 0.18 | 0.28 | 0.38 | 0.48 |
A．电流表A1（量程0.6A，内阻约为1.0Ω）
B．电流表A2（量程3A，内阻约为0.1Ω）
C．电压表V1（量程3V，内阻3kΩ）
D．电压表V2（量程15V，内阻15kΩ）
E．滑动变阻器R1（阻值0～10Ω，额定电流2A）
F．滑动变阻器R2（阻值0～2kΩ，额定电流0.5A）
（1）除长约14cm的中华绘图2B铅笔芯、稳压直流电源E（6V）、开关和带夹子的导线若干外，还需选用的其它器材有ACE（填选项前字母）；
（2）在如图1所示虚线方框中画出实验电路图；
（3）根据表格中数据在图2中画出铅笔芯的I-U图线．
16．我国发射的绕月卫星“嫦娥1号”轨道是圆形的，且贴近月球表面．已知地球质量为月球质量的m倍，地球半径为月球半径的n倍，地球上的第一宇宙速度约为v1，则该探月卫星绕月球运行的速率约为（ ）
| A． | $\sqrt{\frac{n}{m}}{v}_{1}$ | B． | $\sqrt{\frac{m}{n}}{v}_{1}$ | C． | v1 | D． | $\frac{n}{m}{v}_{1}$ |
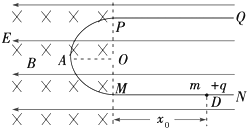在如图所示的竖直平面内有范围足够大、水平向左的匀强电场，在虚线的左侧有垂直纸面向里的匀强磁场，磁感应强度大小为B，一绝缘?形杆由两段直杆和一半径径为R的半圆环组成，固定在纸面所在的竖直平面内，PQ、MN水平且足够长，半圆环MAP在磁场边界左侧，P、M点在磁场边界线上，NMAP段光滑，PQ段粗糙，现在有一质量为m、带电荷量为+q的小环套在MN杆上，它所受电场力为重力的$\frac{1}{2}$倍．现在M点右侧的D点由静止释放小环，小环刚好能到达P点．
20．物体在下列运动过程中，机械能守恒的是（ ）
| A． | 跳伞运动员在空中匀速下落 | B． | 电梯以加速度g向上做匀加速运动 | ||
| C． | 物体在竖直平面内做匀速圆周运动 | D． | 电梯以加速度g向下做匀加速运动 |