题目内容
【题目】如图甲所示,质量为M=3kg,长为2m的木板静止在光滑水平面上,质量也为![]() 的物块以初速度
的物块以初速度![]() 滑上木板的左端,物块与木板之间的动摩擦因数为
滑上木板的左端,物块与木板之间的动摩擦因数为![]() ,在物块滑上木板的同时,给木板施加一个水平向右的恒力F,当恒力F取某一值时,物块在木板上相对于木板滑动的路程为S,给木板施加大小不同的恒力F,得到
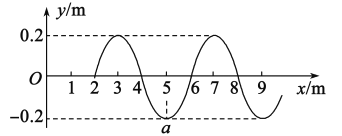
,在物块滑上木板的同时,给木板施加一个水平向右的恒力F,当恒力F取某一值时,物块在木板上相对于木板滑动的路程为S,给木板施加大小不同的恒力F,得到![]() 的关系如图乙所示,其中AB段与横轴平行,且AB段的纵坐标为
的关系如图乙所示,其中AB段与横轴平行,且AB段的纵坐标为![]() .将物块视为质点,最大静摩擦力等于滑动摩擦力,重力加速度
.将物块视为质点,最大静摩擦力等于滑动摩擦力,重力加速度![]() 取
取![]() .
.
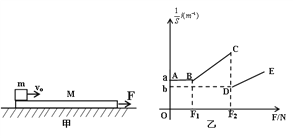
(1)求出乙图中B,D两点的坐标(a,F1);(b,F2)分别是多少?
(2)图乙中BC为直线段,求此直线段![]() 函数关系式.
函数关系式.
【答案】(1)B(![]() ) D(
) D(![]() );(2)
);(2)![]()
【解析】(1)从图中可以看出当F较小时,物块将从木板右端滑下,当F增大到某一值时物块恰好到达木板的右端,且两者具有共同速度,所以a=![]() m
m
以初速度![]() 为正方向,物块的加速度大小:
为正方向,物块的加速度大小: ![]()
木板的加速度大小: ![]()
设经历时间t后两者共速, ![]()
由图乙知,长L=2m ,滑块相对木板的路程: ![]()
可以得出F1=4N
当F继续增大时,物块减速、木板加速,两者在木板上某一位置具有共同速度;当两者共速后能保持相对静止(静摩擦力作用)一起以相同加速度a做匀加速运动;当F再继续增大到F2时两物体达到共速后,将不能一起运动,物体将会从木板的左端滑出。
![]() ,
,
而![]() ,
,
可以求得F2=8N
所以当F2=8N时,物块从vo经过t后与木板的速度相等![]()
![]()
![]()
而此时的相对位移![]()
可以求得![]()
由于物体将会从滑板左侧滑出即![]() ,
,
所以b=![]() 可得坐标:B(
可得坐标:B(![]() ) D(
) D(![]() )
)
(2)当![]() 时,最终两物体达到共速,并最后一起相对静止加速运动,当两者具有共同速度v,历时
时,最终两物体达到共速,并最后一起相对静止加速运动,当两者具有共同速度v,历时![]() ,
,
则: ![]()
![]()
根据速度时间关系可得:
![]()
根据位移关系可得:
![]()
联立![]() 函数关系式解得:
函数关系式解得:
![]()

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目