题目内容
20.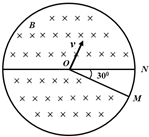 如图所示,在圆形区域中圆心角为30°的扇面MON之外分布着垂直于纸面向里的匀强磁场,磁感应强度大小为B,一质量为m、带电量为-q的粒子,自圆心O点垂直于OM以速度v射入磁场,粒子恰能两次经过边界OM,不计粒子重力.
如图所示,在圆形区域中圆心角为30°的扇面MON之外分布着垂直于纸面向里的匀强磁场,磁感应强度大小为B,一质量为m、带电量为-q的粒子,自圆心O点垂直于OM以速度v射入磁场,粒子恰能两次经过边界OM,不计粒子重力.(1)粒子在磁场区域做圆周运动的轨道半径r
(2)求粒子从O点射入到第一次穿过边界ON的过程中,在磁场中运动的时间t
(3)若粒子第二次经过边界OM时,恰好经过该边界上的P点,求P点到ON的距离h
(4)若圆形区域无限大,现保持其它条件不变而将∠MON变为15°,粒子从O点射出后穿越磁场边界ON和OM的总次数.
分析 (1)粒子,进入磁场后做匀速圆周运动,由洛伦兹力提供向心力,由牛顿第二定律求轨道半径r.
(2)粒子从O点射入到第一次穿过边界ON的过程中,偏转角θ=120°,根据t=$\frac{θ}{360°}$T求时间t.
(3)画出粒子的运动轨迹,由几何关系求解P点到ON的距离h.
(4)将∠MON变为15°,首次从ON边界向下穿出时与之夹角为75°,首次向上穿出OM时与之夹角为60°,每次从边界向扇面区穿出,均比上次夹角减小15°,直到向上穿出时,与ON夹角为15°,不再进入磁场,可得到穿越边界的次数为9次.
解答 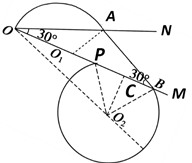 解:(1)由qvB=m$\frac{{v}^{2}}{r}$得 r=$\frac{mv}{qB}$
解:(1)由qvB=m$\frac{{v}^{2}}{r}$得 r=$\frac{mv}{qB}$
(2)粒子第一次穿过边界ON时,偏转角θ=120°
则粒子在磁场中运动的时间 t=$\frac{θ}{360°}$T,其中T=$\frac{2πm}{qB}$
解得:t=$\frac{2πm}{3qB}$.
(3)粒子在磁场中运动轨迹如图所示:
在△O1AB中,O1B=$\frac{{O}_{1}A}{sin30°}$=2r
在△O2PB中,PB=2PC=2rsin30°=r
所以:O1P=O1B-PB=r,OP=OO1+OP=2r
P点到ON的距离 h=OPsin30°=r=$\frac{mv}{qB}$
(4)∠MON变为15°,首次从ON边界向下穿出时与之夹角为75°,首次向上穿出OM时与之夹角为60°,每次从边界向扇面区穿出,均比上次夹角减小15°,直到向上穿出时,与ON夹角为15°,不再进入磁场,故穿越边界的次数为9次.
答:(1)粒子在磁场区域做圆周运动的轨道半径r为$\frac{mv}{qB}$.
(2)粒子从O点射入到第一次穿过边界ON的过程中,在磁场中运动的时间t为$\frac{2πm}{3qB}$.
(3)若粒子第二次经过边界OM时,恰好经过该边界上的P点,P点到ON的距离h为$\frac{mv}{qB}$.
(4)若圆形区域无限大,现保持其它条件不变而将∠MON变为15°,粒子从O点射出后穿越磁场边界ON和OM的总次数为9次.
点评 本题考查带电粒子在磁场中的运动,难度较大,过程复杂,关键在于用运动轨迹图来寻找几何关系,确定长度及角度,将复杂运动形成规律进行简化解决.

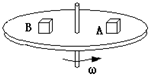 如图所示,A、B两物块置于竖直轴匀速转动的水平圆盘上,A物块距轴较近,两物块始终相对圆盘静止,下列关于两物块的说法,错误的是( )
如图所示,A、B两物块置于竖直轴匀速转动的水平圆盘上,A物块距轴较近,两物块始终相对圆盘静止,下列关于两物块的说法,错误的是( )| A. | 线速度相同 | B. | 周期相同 | C. | 角速度相同 | D. | 转速相同 |
 中国标准粘土砖的尺寸为240×115×53mm,这一尺寸的目的是为了保证砖的长宽高之比为 4:2:1(包括 10mm 的灰缝宽度).可近似认为长宽高分别为 4L、2L、L,现将一块质量为m水平放置的砖块(如图甲)缓慢旋转到竖直放置(如图乙),如果砖块可以视为质量分布均匀,重力加速度为g,则外力至少做的功为( )
中国标准粘土砖的尺寸为240×115×53mm,这一尺寸的目的是为了保证砖的长宽高之比为 4:2:1(包括 10mm 的灰缝宽度).可近似认为长宽高分别为 4L、2L、L,现将一块质量为m水平放置的砖块(如图甲)缓慢旋转到竖直放置(如图乙),如果砖块可以视为质量分布均匀,重力加速度为g,则外力至少做的功为( )| A. | 4mgL | B. | ($\frac{\sqrt{17}}{2}$-$\frac{1}{2}$)mgL | C. | 1.5mgL | D. | ($\frac{\sqrt{5}}{2}$-$\frac{1}{2}$)mgL |
 公路急转弯处通常是交通事故多发地带.如图,某公路急转弯处是一圆弧,当汽车行驶的速率为vc时,汽车恰好没有向公路内外两侧滑动的趋势.则在该弯道处( )
公路急转弯处通常是交通事故多发地带.如图,某公路急转弯处是一圆弧,当汽车行驶的速率为vc时,汽车恰好没有向公路内外两侧滑动的趋势.则在该弯道处( )| A. | 路面外侧高内侧低 | |
| B. | 当路面结冰时,与未结冰时相比,vc的值不变 | |
| C. | 车速只要低于vc,车辆便会受到向内侧的摩擦力 | |
| D. | 车速虽然高于vc,但只要不超出某一最高限度,车辆也不会向外侧滑动 |
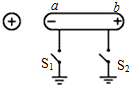 如图所示,把一个带正电的小球放置在原来不带电的枕形导体附近,由于静电感应,枕形导体的a、b端分别出现感应电荷,则( )
如图所示,把一个带正电的小球放置在原来不带电的枕形导体附近,由于静电感应,枕形导体的a、b端分别出现感应电荷,则( )| A. | 枕形导体a端电势高于b端电势 | |
| B. | 仅闭合S1,有电子从大地流向枕形导体 | |
| C. | 仅闭合S1,有电子从枕形导体流向大地 | |
| D. | 仅闭合S2,有正电荷从枕形导体流向大地 |
 ”形木块放在光滑水平地面上,木块水平表面AB粗糙,光滑表面BC与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图乙所示.已知sin37°=0.6,cos37°=0.8,g取10m/s2,求:
”形木块放在光滑水平地面上,木块水平表面AB粗糙,光滑表面BC与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图乙所示.已知sin37°=0.6,cos37°=0.8,g取10m/s2,求: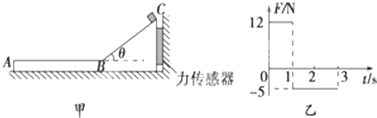
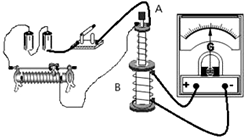 如图为“研究电磁感应现象”的实验装置.如果在闭合开关时发现灵敏电流计的指针向右偏转了一下,那么合上电键稳定后可能出现的情况有:
如图为“研究电磁感应现象”的实验装置.如果在闭合开关时发现灵敏电流计的指针向右偏转了一下,那么合上电键稳定后可能出现的情况有: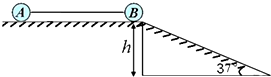 如图所示,光滑水平面与倾角为θ=37°光滑斜面平滑连接,斜面高度为h=5m,质量为mA=3kg的物体A与质量为mB=1kg的物体B通过长为2.5h轻绳连接,开始时,轻绳刚好绷直,物体B位于水平面边缘,由于受到轻微扰动,物体B由静止开始沿斜面下滑,当滑到斜面底端时,由于某种原因轻绳与AB脱离.物体A和B均可看成质点,g取10m/s2.求:(取sin37°=0.6,cos37°=0.8;AB可视为质点.)
如图所示,光滑水平面与倾角为θ=37°光滑斜面平滑连接,斜面高度为h=5m,质量为mA=3kg的物体A与质量为mB=1kg的物体B通过长为2.5h轻绳连接,开始时,轻绳刚好绷直,物体B位于水平面边缘,由于受到轻微扰动,物体B由静止开始沿斜面下滑,当滑到斜面底端时,由于某种原因轻绳与AB脱离.物体A和B均可看成质点,g取10m/s2.求:(取sin37°=0.6,cos37°=0.8;AB可视为质点.)