Question

【题目】一列火车和一辆汽车沿同一方向做匀变速直线运动，速度分别为v1和v2．t=0时刻，火车在汽车前方26m处，此后v1、v2在各个时刻的大小如表所示．根据表格中的数据，通过计算求：

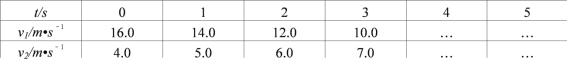
（1）两车经过多长时间相距最大？此时最大间距是多少？

（2）两车初始间距满足什么条件可以相遇两次．

（3）经过多长时间两车相遇？

Answer 1

【答案】（1）4s 50m （2）两车距离小于24m，则两车可以相遇两次．（3）t2=10s

【解析】

（1）由表格知，火车做匀减速直线运动，加速度为：

汽车做匀加速直线运动，加速度为：

开始时，火车的速度大于汽车的速度，并且火车在前，所以两者间距增大，当两者速度相等时，相距最远．设共速所需时间为t，

v′1=v1+a1t=16﹣2t；v′2=v2+a2t=4+t

另v′1=v′2，解得t=4s

此时，火车的位移：

汽车的位移：

两车最大距离：△s=s1+26﹣s2=48+26﹣24m=50m

（2）首先，若要相遇两次，一定要汽车在前．其次，考虑临界情况，如果两车达到共速时，正好相遇，此时：△s′=s1﹣s2=48﹣24m=24m

若两车距离小于这个值，则两车可以相遇两次．

（3）火车做匀减速直线运动，停下来所用的时间为t1：

汽车的位移：

此时，汽车还未追上火车．设t2时刻追上，则：

整理得：

解得：t2=10s