题目内容
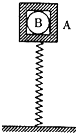 如图所示,一质量不计的轻质弹簧竖立在地面上,弹簧的上端与盒子A连接在一起,下端固定在地面上.盒子内装一个光滑小球,盒子内腔为正方体,一直径略小于此正方体边长的金属圆球B恰好能放在盒内,已知弹簧的劲度系数k=400N/m,A和B的质量均为m=2kg,将A向上提高使弹簧从自由长度开始伸长x1=10cm后,从静止释放,不计空气阻力,A和B一起做竖直方向的简谐运动.取g=10m/s2.已知弹簧处在弹性限度内,对于同一弹簧,其弹性势能只决定于其形变的大小.试求:
如图所示,一质量不计的轻质弹簧竖立在地面上,弹簧的上端与盒子A连接在一起,下端固定在地面上.盒子内装一个光滑小球,盒子内腔为正方体,一直径略小于此正方体边长的金属圆球B恰好能放在盒内,已知弹簧的劲度系数k=400N/m,A和B的质量均为m=2kg,将A向上提高使弹簧从自由长度开始伸长x1=10cm后,从静止释放,不计空气阻力,A和B一起做竖直方向的简谐运动.取g=10m/s2.已知弹簧处在弹性限度内,对于同一弹簧,其弹性势能只决定于其形变的大小.试求:(1)在平衡位置时弹簧的压缩量x2和盒子A的振幅A;
(2)盒子A运动到最高点时,A对B的作用力方向(不要求写出判断的理由);
(3)小球B的最大速度Vm.
分析:(1)振幅是振动物体离开平衡位置的最大距离.当盒子A和金属圆球B所受合力为零时,盒子经过平衡位置,由平衡条件和胡克定律求出此时弹簧压缩的长度.
(2)振子在最高点时速度为零,加速度最大,分析AB运动情况答题.
(3)当盒子运动到平衡位置时,球B的速度最大,根据机械能守恒定律求解金属圆球B的最大速度.
(2)振子在最高点时速度为零,加速度最大,分析AB运动情况答题.
(3)当盒子运动到平衡位置时,球B的速度最大,根据机械能守恒定律求解金属圆球B的最大速度.
解答:解:(1)系统处于平衡位置时,弹簧压缩x2,
A、B处于平衡状态,由平衡条件得:2mg=kx2,
解得,x2=
=
=0.1m;?
盒子的振幅为:H=x1+x2=0.10 m+0.10 m=0.20m;
(2)在最高点,A与B的速度为零,加速度最大,B的重力与A对B的弹力提供B做简谐运动的回复力,A对B的作用力向下.?
(3)小球B运动到平衡位置时速度最大,
从最高点到平衡位置的过程中,弹力做的正功与负功相等,总功为零,
由动能定理,得?2mgA+0+△Ek=
?2m?vm2,?
解得:vm
m/s=2 m/s.?
答:(1)盒子A做简谐运动的振幅为0.20 m;?
(2)盒子A运动到最高点时,盒子A对金属小球B的作用力方向向下;
(3)金属小球B的最大速度为2m/s.?
A、B处于平衡状态,由平衡条件得:2mg=kx2,
解得,x2=
| 2mg |
| k |
| 2×2×10 |
| 400 |
盒子的振幅为:H=x1+x2=0.10 m+0.10 m=0.20m;
(2)在最高点,A与B的速度为零,加速度最大,B的重力与A对B的弹力提供B做简谐运动的回复力,A对B的作用力向下.?
(3)小球B运动到平衡位置时速度最大,
从最高点到平衡位置的过程中,弹力做的正功与负功相等,总功为零,
由动能定理,得?2mgA+0+△Ek=
| 1 |
| 2 |
解得:vm
| 2gA |
答:(1)盒子A做简谐运动的振幅为0.20 m;?
(2)盒子A运动到最高点时,盒子A对金属小球B的作用力方向向下;
(3)金属小球B的最大速度为2m/s.?
点评:对于简谐运动的振幅,往往根据定义去分析求解.本题的技巧在于运用简谐运动的对称性.中等难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
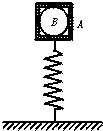 如图所示,一质量不计的轻质弹簧竖立在地面上,弹簧的上端与盒子A连接在一起,下端固定在地面上.盒子A内腔为正方体,一直径略小于此正方体边长的金属圆球B恰好能放在盒内,已知弹簧的劲度系数为k=400N/m,盒子A和金属小球B的质量均为2kg.将盒子A向上提高,使弹簧从自由长度伸长10cm后,由静止释放,不计阻力,盒子A和金属小球B一起做竖直方向的简谐运动,g取10m/s2.已知弹簧处在弹性限度内,对于同一弹簧,其弹性势能只决定于其形变的大小.试求:?
如图所示,一质量不计的轻质弹簧竖立在地面上,弹簧的上端与盒子A连接在一起,下端固定在地面上.盒子A内腔为正方体,一直径略小于此正方体边长的金属圆球B恰好能放在盒内,已知弹簧的劲度系数为k=400N/m,盒子A和金属小球B的质量均为2kg.将盒子A向上提高,使弹簧从自由长度伸长10cm后,由静止释放,不计阻力,盒子A和金属小球B一起做竖直方向的简谐运动,g取10m/s2.已知弹簧处在弹性限度内,对于同一弹簧,其弹性势能只决定于其形变的大小.试求:?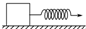 如图所示,一质量不计的弹簧原长为10cm,一端固定于质量m=2kg的物体上,另一端施一水平拉力F.物体与水平面间的动摩擦因数为0.2,(g=10m/s2)
如图所示,一质量不计的弹簧原长为10cm,一端固定于质量m=2kg的物体上,另一端施一水平拉力F.物体与水平面间的动摩擦因数为0.2,(g=10m/s2)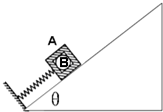 如图所示,一质量不计的轻质弹簧的上端与盒子A连接在一起,盒子A放在倾角为θ=300的光滑固定斜面上,下端固定在斜面上.盒子内装一个光滑小球,盒子内腔为正方体,一直径略小于此正方形边长的金属圆球B恰好能放在盒内,已知弹簧劲度系数为k=100N/m,盒子A和金属圆球B质量均为1kg.,将A沿斜面向上提起,使弹簧从自然长度伸长10cm,从静止释放盒子A,A和B一起在斜面上做简谐振动,g取10m/s2,求:
如图所示,一质量不计的轻质弹簧的上端与盒子A连接在一起,盒子A放在倾角为θ=300的光滑固定斜面上,下端固定在斜面上.盒子内装一个光滑小球,盒子内腔为正方体,一直径略小于此正方形边长的金属圆球B恰好能放在盒内,已知弹簧劲度系数为k=100N/m,盒子A和金属圆球B质量均为1kg.,将A沿斜面向上提起,使弹簧从自然长度伸长10cm,从静止释放盒子A,A和B一起在斜面上做简谐振动,g取10m/s2,求: (2013?普陀区二模)如图所示,一质量不计,可上下自由移动的活塞将理想气体封闭在圆筒内,筒的侧壁为绝缘体,下底M及活塞D均为导体并按图连接,活塞面积S=0.2cm2.闭合电键前,DM间距l1=6μm,闭合电键后,活塞D与下底M分别带有等量异种电荷,并各自产生匀强电场(D与M间的电场为各自产生的电场的叠加).在电场力作用下活塞D发生移动.稳定后,DM间距l2=4μm,此时安培表读数为0.75A,伏特表读数为4V.(大气压强为1.0×105Pa,活塞移动前后气体温度不变,导线对活塞D的作用力不计).以下说法正确的是( )
(2013?普陀区二模)如图所示,一质量不计,可上下自由移动的活塞将理想气体封闭在圆筒内,筒的侧壁为绝缘体,下底M及活塞D均为导体并按图连接,活塞面积S=0.2cm2.闭合电键前,DM间距l1=6μm,闭合电键后,活塞D与下底M分别带有等量异种电荷,并各自产生匀强电场(D与M间的电场为各自产生的电场的叠加).在电场力作用下活塞D发生移动.稳定后,DM间距l2=4μm,此时安培表读数为0.75A,伏特表读数为4V.(大气压强为1.0×105Pa,活塞移动前后气体温度不变,导线对活塞D的作用力不计).以下说法正确的是( )