题目内容
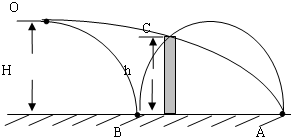
如图所示,竖直平面内有一粗糙的圆弧圆管轨道,其半径为R=0.5m,内径很小.平台高h=1.9m,一质量m=0.5kg、直径略小于圆管内径的小球,从平台边缘的A处水平射出,恰能沿圆管轨道上P点的切线方向进入圆管内,轨道半径OP与竖直线的夹角为37°.g=10m/s2,sin37°=0.6,cos37°=0.8.不计空气阻力.求:
(1)小球从平台上的A点射出时的速度v0是多大?
(2)小球通过最高点Q时,圆管轨道对小球向下的压力FQ=3N,小球在圆管轨道中运动时克服阻力所做的功W是多少?

(1)小球从平台上的A点射出时的速度v0是多大?
(2)小球通过最高点Q时,圆管轨道对小球向下的压力FQ=3N,小球在圆管轨道中运动时克服阻力所做的功W是多少?

(1)设小球抛出后做平抛运动至P,
竖直位移y=h-R(1-cos37°)
由y=
gt2
知平抛用时t=
=0.6s
小球达P点竖直速度小球达P点竖直速度vy=gt=6m/s
小球恰沿P点切线方向进入圆管,由速度关系:
tanθ=
小球从平台上的A点射出时的速度v0=
=8m/s;
(2)小球在P点速度vp=
=10m/s
小球在圆周Q点,由牛顿第二定律:
mg+FQ=m
小球由P运动到Q过程,上升高度H=R+Rcos37°=0.9m
由动能定理:
-mgH-W=
m
-
m
联立解得,小球在圆管轨道中运动时克服阻力所做的功
W=18.5J.
答:(1)小球从平台上的A点射出时的速度v0是8m/s;
(2)小球在圆管轨道中运动时克服阻力所做的功W是18.5J.
竖直位移y=h-R(1-cos37°)
由y=
| 1 |
| 2 |
知平抛用时t=
|
小球达P点竖直速度小球达P点竖直速度vy=gt=6m/s
小球恰沿P点切线方向进入圆管,由速度关系:
tanθ=
| vy |
| vx |
小球从平台上的A点射出时的速度v0=
| vy |
| tan37° |
(2)小球在P点速度vp=
|
小球在圆周Q点,由牛顿第二定律:
mg+FQ=m
| ||
| R |
小球由P运动到Q过程,上升高度H=R+Rcos37°=0.9m
由动能定理:
-mgH-W=
| 1 |
| 2 |
| v | 2Q |
| 1 |
| 2 |
| v | 2p |
联立解得,小球在圆管轨道中运动时克服阻力所做的功
W=18.5J.
答:(1)小球从平台上的A点射出时的速度v0是8m/s;
(2)小球在圆管轨道中运动时克服阻力所做的功W是18.5J.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目