题目内容
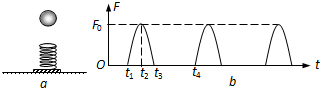
如图(a)所示，质量m=1 kg的物体沿倾角θ=37°的固定粗糙斜面由静止开始向下运动，风对物体的作用力沿水平方向向右，其大小与风速v成正比，比例系数用k表示，物体的加速度a与风速v的关系如图(b)所示， （sin37°=0.6，cos37°=0.8，g取10 m/s2）求：
(1)物体与斜面间的动摩擦因数μ；
(2)比例系数k。
(1)物体与斜面间的动摩擦因数μ；
(2)比例系数k。
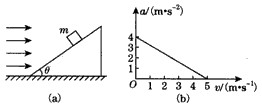
解：(1)由题图知v=0时，a0=4 m/s2
由牛顿第二定律得：mgsinθ-μmgcosθ=ma0
解得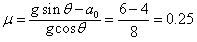
(2)由题图知v=5m/s时，a=0
由平衡条件得：mgsinθ-μFN-kvcosθ=0，FN=mgcosθ十kvsinθ
联立两式得：mg(sinθ-μcosθ)-kv(μsinθ+cosθ)=0
解得k=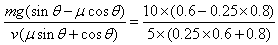
kg/s=0.84 kg/s
由牛顿第二定律得：mgsinθ-μmgcosθ=ma0
解得
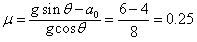
(2)由题图知v=5m/s时，a=0
由平衡条件得：mgsinθ-μFN-kvcosθ=0，FN=mgcosθ十kvsinθ
联立两式得：mg(sinθ-μcosθ)-kv(μsinθ+cosθ)=0
解得k=
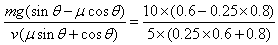kg/s=0.84 kg/s
练习册系列答案
相关题目
如图a所示，质量为m的物体放在倾角θ=30°的粗糙斜面上，现在用与斜面底边平行、大小为F=
如图a所示，质量分布均匀、长宽分别为a、b的长方体木块ABCD，左上角用光滑的铰链与固定装置连接，底部放一个厚度与长方体宽度相同的小物块，小物块放在光滑水平面将木块支撑起来，长方体木块的质量为m，其底边DC与水平面平行，与小物块之间的动摩擦因素为μ．现用水平向右的力F将小物块从D匀速拉至C处．