题目内容
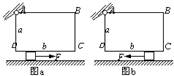
 如图a所示,质量分布均匀、长宽分别为a、b的长方体木块ABCD,左上角用光滑的铰链与固定装置连接,底部放一个厚度与长方体宽度相同的小物块,小物块放在光滑水平面将木块支撑起来,长方体木块的质量为m,其底边DC与水平面平行,与小物块之间的动摩擦因素为μ.现用水平向右的力F将小物块从D匀速拉至C处.
如图a所示,质量分布均匀、长宽分别为a、b的长方体木块ABCD,左上角用光滑的铰链与固定装置连接,底部放一个厚度与长方体宽度相同的小物块,小物块放在光滑水平面将木块支撑起来,长方体木块的质量为m,其底边DC与水平面平行,与小物块之间的动摩擦因素为μ.现用水平向右的力F将小物块从D匀速拉至C处.(1)推导出拉力F的大小随小物块距D点距离x的关系式.
(2)如果用水平力F将小物块从C向D方向拉动(如图b),请通过理论推导,推测将发生什么情况?
分析:(1)对长方体受力分析,通过力矩平衡求出摩擦力与x的关系,抓住拉力F与摩擦力相等求出D大小与小物块距D点距离x的关系式.
(2)根据力矩平衡得出拉力与x的关系,然后进行判断.
(2)根据力矩平衡得出拉力与x的关系,然后进行判断.
解答:解:(1)对长方体木块受力分析,并根据力矩平衡条件有:mg
=f?a+N?x f=μN
?F=f=
?
(2 ) 当用向左的力拉小物块时,长方体木块所受的摩擦力方向与(1)的分析相反.故有:mg
+f?a=N?x
F=f=
,随着小物块的向左运动,x减小,当x→μ.a,F→∞,由此推测:物体将无法移动,产生自锁现象.
答:(1)拉力F的大小随小物块距D点距离x的关系式为
.
(2)物体将无法移动,产生自锁现象.
| b |
| 2 |

?F=f=
| μmgb |
| 2(μa+x) |
(2 ) 当用向左的力拉小物块时,长方体木块所受的摩擦力方向与(1)的分析相反.故有:mg
| b |
| 2 |
F=f=
| μmgb |
| 2(x-μa) |
答:(1)拉力F的大小随小物块距D点距离x的关系式为
| μmgb |
| 2(μa+x) |
(2)物体将无法移动,产生自锁现象.
点评:解决本题的关键抓住长方体木块力矩平衡进行求解.

练习册系列答案
相关题目
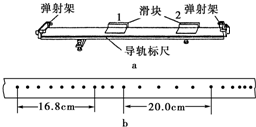 (2009?肇庆一模)某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验.气垫导轨装置如图a所示,所用的气垫导轨装置由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差.
(2009?肇庆一模)某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验.气垫导轨装置如图a所示,所用的气垫导轨装置由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差.