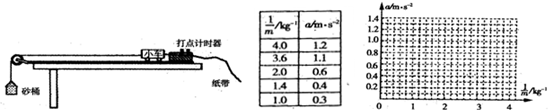
��Ŀ����
����ͼ��ʾ��ʵ��װ����֤��е���غ㶨�ɣ�ʵ�����õĵ�ԴΪѧ����Դ�������ѹΪ6V�Ľ������ֱ�������֣��ش��Ӹߴ��ɾ�ֹ��ʼ���䣬�ش������ŵ�ֽ�����һϵ�еĵ㣬��ֽ���ϵĵ㼣���в�����������������֤��е���غ㶨�ɣ�
��1�������о��˸�ʵ��ļ����������裺
A������ͼʾ��װ�ð�װ������
B��������ʱ���ӵ���Դ�ġ�ֱ�����ϣ�
C�����ͷ�ֽ�����ٽ�ͨ��Դ���һ��ֽ����
D������ֽ����ijЩ���ľ��룻
E�����ݲ����Ľ�����ֱ�����ش���������м��ٵ��������ܺ����ӵĶ��ܣ�
���в��������IJ����ǣ� ����ѡ���Ӧ����ĸ��
��2����ȷ����������ֽ����ͼ��ʾ�����ݴ����ֽ����ѡȡֽ���������������A��B��C��D��E�����AC�ľ���Ϊs1��CE�ľ���Ϊs2������Ƶ��Ϊf��������Щ�����������C��ʱ�ش����������vc=
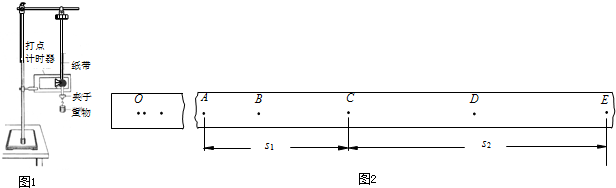
��3��ʵ���з��֣��ش���С���������ܴ����ش����ܵ�����������Ҫԭ�������ش�����Ĺ����д����������ã��������㶨��������ͨ����ʵ��װ�ò������Ĵ�С������֪�����������ٶ�Ϊg���ش�������Ϊm��������Щ����������ͼֽ���ϵ����ݷ��ű�ʾ���ش�������������ܵ���������СF= ��
��1�������о��˸�ʵ��ļ����������裺
A������ͼʾ��װ�ð�װ������
B��������ʱ���ӵ���Դ�ġ�ֱ�����ϣ�
C�����ͷ�ֽ�����ٽ�ͨ��Դ���һ��ֽ����
D������ֽ����ijЩ���ľ��룻
E�����ݲ����Ľ�����ֱ�����ش���������м��ٵ��������ܺ����ӵĶ��ܣ�
���в��������IJ����ǣ�
��2����ȷ����������ֽ����ͼ��ʾ�����ݴ����ֽ����ѡȡֽ���������������A��B��C��D��E�����AC�ľ���Ϊs1��CE�ľ���Ϊs2������Ƶ��Ϊf��������Щ�����������C��ʱ�ش����������vc=

��3��ʵ���з��֣��ش���С���������ܴ����ش����ܵ�����������Ҫԭ�������ش�����Ĺ����д����������ã��������㶨��������ͨ����ʵ��װ�ò������Ĵ�С������֪�����������ٶ�Ϊg���ش�������Ϊm��������Щ����������ͼֽ���ϵ����ݷ��ű�ʾ���ش�������������ܵ���������СF=
���������ʵ����������Ҫ���ո�ʵ��ԭ�����˽�ʵ���������������������ݴ����Լ�ע�����
ֽ����ʵ���У���ֽ���ȱ���ֱ���˶������ֽ���ϵĵ��࣬�����ȱ���ֱ���˶������ۣ��ɼ�������ij��ʱֽ���˶���˲ʱ�ٶȺͼ��ٶȣ��Ӷ�������ܣ�
����ţ�ٵڶ��������������
ֽ����ʵ���У���ֽ���ȱ���ֱ���˶������ֽ���ϵĵ��࣬�����ȱ���ֱ���˶������ۣ��ɼ�������ij��ʱֽ���˶���˲ʱ�ٶȺͼ��ٶȣ��Ӷ�������ܣ�
����ţ�ٵڶ��������������
����⣺��1�����в��������IJ����ǣ�BC
B����͵�ż�ʱ����ʹ�ý�����Դ��
C��ʵ��ʱ��Ӧ���ͷ�����ٽ�ͨ����ʱ����Դ�����������˶��Ͽ죬���ܻ�ʹ������ĵ���٣����������ݵIJɼ��ʹ�����
��2�������ȱ���ֱ���˶�������v
=
vC=
=
=
��3�������ȱ���ֱ���˶������ۡ�x=at2
a=
=
����������ţ�ٵڶ����ɵã�
mg-f=ma
f=mg-ma=m[g-
]��
�ʴ�Ϊ����1��BC
��2��
��3��m[g-
]��
B����͵�ż�ʱ����ʹ�ý�����Դ��
C��ʵ��ʱ��Ӧ���ͷ�����ٽ�ͨ����ʱ����Դ�����������˶��Ͽ죬���ܻ�ʹ������ĵ���٣����������ݵIJɼ��ʹ�����
��2�������ȱ���ֱ���˶�������v
| t |
| 2 |
. |
| v |
vC=
| xAE |
| tAE |
| s1+s2 |
| 4T |
| (s1+s2)f |
| 4 |
��3�������ȱ���ֱ���˶������ۡ�x=at2
a=
| s2-s1 |
| (2T)2 |
| (s2-s1)f2 |
| 4 |
����������ţ�ٵڶ����ɵã�
mg-f=ma
f=mg-ma=m[g-
| (s2-s1)f2 |
| 4 |
�ʴ�Ϊ����1��BC
��2��
| (s1+s2)f |
| 4 |
��3��m[g-
| (s2-s1)f2 |
| 4 |
������ֽ������Ĵ���ʱ��ѧʵ���г��������⣮���ǿ���ֽ����ʵ���У���ֽ���ȱ���ֱ���˶������ֽ���ϵĵ��࣬�����ȱ���ֱ���˶������ۣ��ɼ�������ij��ʱֽ���˶���˲ʱ�ٶȺͼ��ٶȣ�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ����ͼ��ʾ��ʵ��װ����֤��е���غ㶨�ɣ�ʵ�����õĵ�ԴΪѧ����Դ�������ѹΪ6V�Ľ������ֱ�������֣��ش��Ӹߴ��ɾ�ֹ��ʼ���䣬�ش������ŵ�ֽ�����һϵ�еĵ㣬��ֽ���ĵ�۽��в�����������֤��е���غ㶨�ɣ�
����ͼ��ʾ��ʵ��װ����֤��е���غ㶨�ɣ�ʵ�����õĵ�ԴΪѧ����Դ�������ѹΪ6V�Ľ������ֱ�������֣��ش��Ӹߴ��ɾ�ֹ��ʼ���䣬�ش������ŵ�ֽ�����һϵ�еĵ㣬��ֽ���ĵ�۽��в�����������֤��е���غ㶨�ɣ�
 С��ͬѧ����ͼ��ʾ��ʵ��װ����֤���ɣ���������һ��������ٶ������ܺ��������ȣ�
С��ͬѧ����ͼ��ʾ��ʵ��װ����֤���ɣ���������һ��������ٶ������ܺ��������ȣ�
 ����ͼ��ʾ��ʵ��װ�ù۲�˫�����ͼ����˫��֮��ľ�����0.3mm���õ��Ǻ�ɫ��ɫƬ����ë�������Ͽ��Կ�����ɫ�������ƣ�
����ͼ��ʾ��ʵ��װ�ù۲�˫�����ͼ����˫��֮��ľ�����0.3mm���õ��Ǻ�ɫ��ɫƬ����ë�������Ͽ��Կ�����ɫ�������ƣ�
 ����ͼ��ʾ��ʵ��װ����֤��е���غ㶨�ɣ�ʵ�����õĵ�ԴΪѧ����Դ�������ѹΪ6V�Ľ������ֱ�������֣��ش��Ӹߴ��ɾ�ֹ��ʼ���䣬�ش������ŵ�ֽ�����һϵ�еĵ㣬��ֽ���ϵĵ㼣���в�����������֤��е���غ㶨�ɣ�
����ͼ��ʾ��ʵ��װ����֤��е���غ㶨�ɣ�ʵ�����õĵ�ԴΪѧ����Դ�������ѹΪ6V�Ľ������ֱ�������֣��ش��Ӹߴ��ɾ�ֹ��ʼ���䣬�ش������ŵ�ֽ�����һϵ�еĵ㣬��ֽ���ϵĵ㼣���в�����������֤��е���غ㶨�ɣ�