��Ŀ����
11���ڹ�������ˮ���ϰ�װˮƽ���ʹ���������б�滬�µĹ�����ˮƽ���ʹ����д��ͣ��ɴ����߹���Ч�ʣ���ͼ��ʾ��һ���30��Ĺ⻬б���¶���ˮƽ���ʹ�������һ������h=0.2m�ߴ���A���ɾ�ֹ���º�B����ٶ�Ϊv1��������v1����ˮƽ���õĴ��ʹ�����֪�����ʹ���L=7m�����ұ���v0=4m/s�������ٶȲ��䣬�����봫�ʹ���Ķ�Ħ��������=0.2�������������ƣ��������ٶ�gȡ10m/s2�������ɿ����ʵ㣮��
��1���»���B����ٶ�V1���ڶ��٣�
��2������A���ɾ�ֹ�»����뿪���ʹ�C�����õ�ʱ�䣮
��3�����贫�ʹ��ǰ�ɫ�ģ�����Ϊһú�飬����B����C�Ĺ����У��ڴ��ʹ������º�ɫ�ۼ��ij��ȣ�
���� ��1�����ݶ��ܶ�����������»���B����ٶȴ�С��
��2������ţ�ٵڶ����ɺ��ٶ�ʱ�乫ʽ���������б���ϵ��˶�ʱ�䣬����ţ�ٵڶ����ɺ��˶�ѧ��ʽ����ڴ��ʹ����ȼ����˶���ʱ���λ�ƣ��Ӷ��ó������˶���λ�ƣ���������˶���ʱ�䣬�Ӷ��ó���ʱ�䣮
��3������Ի����Ĺ����У���ϴ��ʹ���λ�ƺ�����λ�������Ի�����λ�ƴ�С������ɫ�ۼ��ij��ȣ�
��� �⣺��1�����ݶ��ܶ����ã�$mgh=\frac{1}{2}m{{v}_{1}}^{2}$��
��ã�${v}_{1}=\sqrt{2gh}=\sqrt{2��10��0.2}$m/s=2m/s��
��2����б�����»��ļ��ٶ�Ϊ��${a}_{1}=gsin��=10��\frac{1}{2}m/{s}^{2}=5m/{s}^{2}$��
����б���ϵ��˶�ʱ��Ϊ��${t}_{1}=\frac{{v}_{1}}{{a}_{1}}=\frac{2}{5}s=0.4s$��
�ڴ��ʹ������ȼ����˶���ʱ��Ϊ��${t}_{2}=\frac{{v}_{0}-{v}_{1}}{{a}_{2}}=\frac{4-2}{0.2��10}s=1s$��
�ȼ����˶���λ��Ϊ��${x}_{1}=\frac{{{v}_{0}}^{2}-{{v}_{1}}^{2}}{2{a}_{2}}=\frac{16-4}{2��2}m=3m$��
�����˶���ʱ��Ϊ��${t}_{3}=\frac{L-{x}_{1}}{{v}_{0}}=\frac{7-3}{4}s=1s$��
����A���ɾ�ֹ�»����뿪���ʹ�C�����õ�ʱ��Ϊ��t=t1+t2+t3=0.4+1+1s=2.4s��
��3���ڴ��ʹ������º�ɫ�ۼ��ij���Ϊ����x=v0t2-x1=4��1-3m=1m��
�𣺣�1������B����ٶ�V1����2m/s��
��2��������A���ɾ�ֹ�»����뿪���ʹ�C�����õ�ʱ��Ϊ2.4s��
��3��������B����C�Ĺ����У��ڴ��ʹ������º�ɫ�ۼ��ij���Ϊ1m��
���� �������Ĺؼ�����������ڴ��ʹ��ϵ��˶����ɣ����ţ�ٵڶ����ɺ��˶�ѧ��ʽ������⣮

| A�� | 2m/s��3m/s��4m/s | B�� | 2m/s��4m/s��6m/s | C�� | 3m/s��4m/s��5m/s | D�� | 3m/s��5m/s��7m/s |
| A�� | ¯�ڿ��� | B�� | ���� | C�� | ���� | D�� | ͬʱ������ |

 �ռ�������A��B��Cλ��ֱ�������ε��������㣬��AB=4cm��BC=3cm���ֽ�����QA��QB�ֱ����A��B���㣬���C��ij�ǿΪEC=10V/m��������ͼ��ʾ����
�ռ�������A��B��Cλ��ֱ�������ε��������㣬��AB=4cm��BC=3cm���ֽ�����QA��QB�ֱ����A��B���㣬���C��ij�ǿΪEC=10V/m��������ͼ��ʾ���� ��1��ƽ��������˶����ɿ��Ը���Ϊ���㣺һ��ˮƽ�����������˶���������ֱ���������������˶���Ϊ���о�ƽ��������˶������������ʵ�飺��ͼ1��ʾ����С��������Խ���Ƭ��A���ˮƽ�ɳ���ͬʱB���ɿ��������������˶�����������ͬʱ�䵽���棬�����ʵ��B
��1��ƽ��������˶����ɿ��Ը���Ϊ���㣺һ��ˮƽ�����������˶���������ֱ���������������˶���Ϊ���о�ƽ��������˶������������ʵ�飺��ͼ1��ʾ����С��������Խ���Ƭ��A���ˮƽ�ɳ���ͬʱB���ɿ��������������˶�����������ͬʱ�䵽���棬�����ʵ��B ����ͼ��ʾ�ĸ�ͼ�У��ֱ�����˵����еĵ��������ų���ij��С����N����ָ���Ÿ��߷����뻭����Ӧ�ĴŸ��ߣ����Ϸ����������
����ͼ��ʾ�ĸ�ͼ�У��ֱ�����˵����еĵ��������ų���ij��С����N����ָ���Ÿ��߷����뻭����Ӧ�ĴŸ��ߣ����Ϸ����������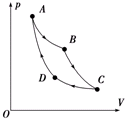 ��ͼ��ʾ��һ�����������������״̬A���ξ���״̬B��C��D���ٻص�״̬A�����У�A��B��C��DΪ���¹��̣�B��C��D��AΪ���ȹ��̣����������������������������������ġ���ŵѭ������
��ͼ��ʾ��һ�����������������״̬A���ξ���״̬B��C��D���ٻص�״̬A�����У�A��B��C��DΪ���¹��̣�B��C��D��AΪ���ȹ��̣����������������������������������ġ���ŵѭ������