题目内容
14. 如图1用同种材料制成倾角37°的斜面和长水平面,斜面长15m且固定,一小物块从斜面顶端以沿斜面向下的初速度v0开始自由下滑,当v0=2m/s时,经过5s后小物块停在斜面上.多次改变v0的大小,记录下小物块从开始运动到最终停下的时间t,作出t-v0图象,如图2所示,g=10m/s2 求:
如图1用同种材料制成倾角37°的斜面和长水平面,斜面长15m且固定,一小物块从斜面顶端以沿斜面向下的初速度v0开始自由下滑,当v0=2m/s时,经过5s后小物块停在斜面上.多次改变v0的大小,记录下小物块从开始运动到最终停下的时间t,作出t-v0图象,如图2所示,g=10m/s2 求:(1)小物块与该种材料间的动摩擦因数为多少?
(2)某同学认为,若小物块初速度为4m/s,则根据图象中t与v0成正比推导,可知小物块运动时间为10s.以上说法是否正确?若不正确,说明理由并解出你认为正确的结果.
分析 (1)根据t-v0图象,求出小物块的加速度,物块做匀减速直线运动,根据牛顿第二定律有 ma=μmgcosθ-mgsinθ,求出动摩擦因数.
(2)初速度增大后,物块会滑动水平面上,水平面上运动的加速度和斜面上运动的加速度不同,规律将不再符合图象中的正比关系.
先讨论是否还停在斜面上.若不停在斜面上,先求出滑动斜面底端的速度和时间,再通过水平面上的加速度,求出在水平面上运动的时间,从而得出小物块从开始运动到最终停下的时间t.
解答 解:(1)由加速度的定义式:a=$\frac{△v}{△t}=\frac{2}{5}=0.4$m/s2
ma=μmgcosθ-mgsinθ
代入数据得:μ=0.8
(2)不正确.因为随着初速度增大,小物块会滑到水平面,规律将不再符合图象中的正比关系;
v0=4m/s时,若保持匀减速下滑,则经过s=$\frac{{v}_{0}^{2}}{2a}$=$\frac{{4}^{2}}{2×0.4}$=20m>15m,已滑到水平面
物体在斜面上运动,设刚进入水平面时速度v1:${{v}_{1}}^{2}-{{v}_{0}}^{2}=2a{s}_{斜}$,${t}_{1}=\frac{{v}_{1}-{v}_{0}}{a}$,得v1=2m/s,t1=5s
水平面上${t}_{2}=\frac{{v}_{1}}{μg}=\frac{2}{0.8×10}=0.25s$
总时间t1+t2=5.25s
答:(1)小物块与该种材料间的动摩擦因数为0.8;
(2)不正确.因为随着初速度增大,小物块会滑到水平面,规律将不再符合图象中的正比关系;小物块运动的时间是5.25s.
点评 解决本题的关键知道速度增大到一定程度后,物块不会停留在斜面上,会停留在水平面上,根据牛顿第二定律,分别求出在斜面上和水平面上运动的加速度,从而求出两段时间之和.

 阅读快车系列答案
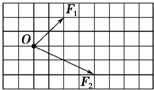
阅读快车系列答案 如图所示,6个力的合力为F1,若去掉1N的那个分力,则其余5个力的合力为F2.则关于F1、F2的大小及方向表述正确的是( )
如图所示,6个力的合力为F1,若去掉1N的那个分力,则其余5个力的合力为F2.则关于F1、F2的大小及方向表述正确的是( )| A. | F1=0,F2=0 | B. | F1=1N,方向与1N的力反向,F2=0 | ||
| C. | F1=0,F2=1N,方向与4N的力同向 | D. | F1=0,F2=7N,方向与4N的力同向 |
 2012年10月15日,奥地利著名极限运动员鲍姆加特纳从距地面高度约3.9万米的高空跳下,并成功着陆.假设他沿竖直方向下落,其v-t图象如图所示,则下列说法中正确的是( )
2012年10月15日,奥地利著名极限运动员鲍姆加特纳从距地面高度约3.9万米的高空跳下,并成功着陆.假设他沿竖直方向下落,其v-t图象如图所示,则下列说法中正确的是( )| A. | 0~t1时间内运动员及其装备机械能守恒 | |
| B. | t1~t2时间内运动员处于超重状态 | |
| C. | t1~t2时间内运动员的平均速度v=$\frac{{v}_{1}+{v}_{2}}{2}$ | |
| D. | t2~t4时间内重力对运动员所做的功等于他克服阻力所做的功 |
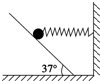 如图所示,质量为m的小球用水平轻质弹簧系住,并用倾角θ=37°的木板托住,小球处于静止状态,弹簧处于压缩状态,则( )
如图所示,质量为m的小球用水平轻质弹簧系住,并用倾角θ=37°的木板托住,小球处于静止状态,弹簧处于压缩状态,则( )| A. | 小球受木板的摩擦力一定沿斜面向上 | |
| B. | 弹簧弹力不可能为$\frac{3}{4}$mg | |
| C. | 小球可能受三个力作用 | |
| D. | 木板对小球的作用力有可能小于小球的重力mg |
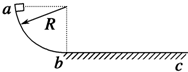 如图所示,在光滑四分之一圆弧轨道的顶端a点,质量为m的物块(可视为质点)由静止开始下滑,经圆弧最低点b滑上粗糙水平面,圆弧轨道在b点与水平轨道平滑相接,物块最终滑至c点停止.若圆弧轨道半径为R,物块与水平面间的动摩擦因数为μ,下列说法错误的是( )
如图所示,在光滑四分之一圆弧轨道的顶端a点,质量为m的物块(可视为质点)由静止开始下滑,经圆弧最低点b滑上粗糙水平面,圆弧轨道在b点与水平轨道平滑相接,物块最终滑至c点停止.若圆弧轨道半径为R,物块与水平面间的动摩擦因数为μ,下列说法错误的是( )| A. | 物块滑到b点时的速度为$\sqrt{gR}$ | B. | 物块滑到b点时对b点的压力是3mg | ||
| C. | c点与b点的距离为$\frac{R}{μ}$ | D. | 整个过程中物块机械能损失了mgR |
| 电热水壶 | |||
| 型号 | SP-356A | 额定电压 | 220V |
| 额定功率 | 1 800W | 额定频率 | 50Hz |
| 额定容量 | 1.5L | ||
| A. | 1.80×103 J | B. | 1.10×104 J | C. | 1.32×104 J | D. | 1.08×105 J |
| A. | 新闻30分每天中午12点开播 | B. | 一场足球比赛用时90分钟 | ||
| C. | 火车运行3小时15分 | D. | 数学测试的时间是45分钟 |
 在“探究力的平行四边形定则”实验中,需要将橡皮条的一端固定在水平木板上,先用一个弹簧秤拉橡皮条的另一端到某一点并记下该点的位置;再将橡皮条的另一端系两根细绳,细绳的另一端都有绳套,用两个弹簧秤分别勾住绳套,并互成角度地拉橡皮条.
在“探究力的平行四边形定则”实验中,需要将橡皮条的一端固定在水平木板上,先用一个弹簧秤拉橡皮条的另一端到某一点并记下该点的位置;再将橡皮条的另一端系两根细绳,细绳的另一端都有绳套,用两个弹簧秤分别勾住绳套,并互成角度地拉橡皮条. 已知物块重G=10N,斜面倾角为θ=37°,若接触面间动摩擦因数μ=0.8,最大静摩擦力等于滑动摩擦力,给物块施加一沿斜面方向的力F,使物块能沿斜面匀速滑动,求力F的方向和大小?
已知物块重G=10N,斜面倾角为θ=37°,若接触面间动摩擦因数μ=0.8,最大静摩擦力等于滑动摩擦力,给物块施加一沿斜面方向的力F,使物块能沿斜面匀速滑动,求力F的方向和大小?