题目内容
6.α粒子(${\;}_{2}^{4}$He)和氘核(${\;}_{1}^{2}$H)垂直于磁感线方向进入同一匀强磁场中,它们作匀速圆周运动的半径相同,其原因可能是它们( )| A. | 进入磁场的初速度相同 | |
| B. | 进入磁场的初动能相同 | |
| C. | 入磁场的初动量相同 | |
| D. | 进入磁场前均由静止起经同一电场加速 |
分析 明确α粒子(${\;}_{2}^{4}$He)和氘核(${\;}_{1}^{2}$H)的比荷相等;
再根据带电粒子射入同一匀强磁场作匀速圆周运动,由洛伦兹力提供向心力,由牛顿第二定律和圆周运动的规律得到半径公式,即可进行分析速度、动量和动能关系.
再根据带电粒子在电场中的加速规律可明确是否经同一电场加速.
解答 解:α粒子(${\;}_{2}^{4}$He)和氘核(${\;}_{1}^{2}$H)的比荷相等;
带电粒子在匀强磁场中作匀速圆周运动,由洛伦兹力提供向心力,由牛顿第二定律得:
qvB=m$\frac{{v}^{2}}{r}$
得:r=$\frac{mv}{qB}$,
r相等,B相等,比荷相等,则可知两粒子的初速度一定相等;初动能及初动量均可能不相等;
由Uq=$\frac{1}{2}$mv2可知,v=$\sqrt{\frac{2Uq}{m}}$,因比荷相同,则说明加速电压相同;故说明它们是经同一电场加速进入磁场的;
故AD正确,BC错误;
故选:AD.
点评 本题考查带电粒子在电场中的加速问题;而推导带电粒子在磁场中匀速圆周运动的半径的基本思路是:洛伦兹力提供向心力,实质就是牛顿第二定律的具体应用.

练习册系列答案
相关题目
18.关于电场线,下列说法中正确的有( )
| A. | 电场线上每一点的切线方向表示电荷通过时的运动方向 | |
| B. | 沿电场线方向,电场强度逐渐减小 | |
| C. | 电场线越密的地方,电荷所受的电场力一定越大 | |
| D. | 只受电场力作用的点电荷,在电场中可能做匀速圆周运动 |
17.下列说法正确的是( )
| A. | 硬币漂浮在水面上,主要是因为硬币受到水的浮力的作用 | |
| B. | 一定质量理想气体在等压变化时,若升高相同的温度,则增加的体积一定相同 | |
| C. | 分子间的引力和斥力,都随着分子间距离的增大而减小 | |
| D. | 分子间距离减小时,分子间的势能可能增大 |
1.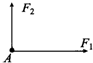 如图所示,质点A受到F1和F2两个力的作用,其中F1=8N;F2=6N,方向与F1垂直,这两个力的合力的大小F=( )N.
如图所示,质点A受到F1和F2两个力的作用,其中F1=8N;F2=6N,方向与F1垂直,这两个力的合力的大小F=( )N.
 如图所示,质点A受到F1和F2两个力的作用,其中F1=8N;F2=6N,方向与F1垂直,这两个力的合力的大小F=( )N.
如图所示,质点A受到F1和F2两个力的作用,其中F1=8N;F2=6N,方向与F1垂直,这两个力的合力的大小F=( )N.| A. | 10N | B. | 14N | C. | 2N | D. | 无法判断 |
11. 如图所示,用两支相同的弹簧秤吊着一根铜棒,铜棒所在的虚线框范围内有垂直纸面的匀强磁场,棒中通入自左向右的电流.当棒静止时,两弹簧秤示数均为F1;若将棒中电流反向而保持大小不变,当棒静止时,两弹簧秤的示数均为F2,且F2>F1,根据上面所给的信息不能求出( )
如图所示,用两支相同的弹簧秤吊着一根铜棒,铜棒所在的虚线框范围内有垂直纸面的匀强磁场,棒中通入自左向右的电流.当棒静止时,两弹簧秤示数均为F1;若将棒中电流反向而保持大小不变,当棒静止时,两弹簧秤的示数均为F2,且F2>F1,根据上面所给的信息不能求出( )
 如图所示,用两支相同的弹簧秤吊着一根铜棒,铜棒所在的虚线框范围内有垂直纸面的匀强磁场,棒中通入自左向右的电流.当棒静止时,两弹簧秤示数均为F1;若将棒中电流反向而保持大小不变,当棒静止时,两弹簧秤的示数均为F2,且F2>F1,根据上面所给的信息不能求出( )
如图所示,用两支相同的弹簧秤吊着一根铜棒,铜棒所在的虚线框范围内有垂直纸面的匀强磁场,棒中通入自左向右的电流.当棒静止时,两弹簧秤示数均为F1;若将棒中电流反向而保持大小不变,当棒静止时,两弹簧秤的示数均为F2,且F2>F1,根据上面所给的信息不能求出( )| A. | 安培力的大小 | B. | 磁场的方向 | ||
| C. | 铜棒的重力 | D. | 磁感应强度的大小 |
18.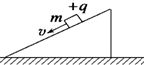 如图所示,倾角为θ的绝缘斜面固定在水平面上,当质量为m,带电荷量为+q的滑块以速度v沿斜面匀速下滑时,在此空间突然加上方向沿斜面向下的匀强电场E,且Eq=mg,滑块继续沿斜面滑动距离L到达斜面底端.则( )
如图所示,倾角为θ的绝缘斜面固定在水平面上,当质量为m,带电荷量为+q的滑块以速度v沿斜面匀速下滑时,在此空间突然加上方向沿斜面向下的匀强电场E,且Eq=mg,滑块继续沿斜面滑动距离L到达斜面底端.则( )
 如图所示,倾角为θ的绝缘斜面固定在水平面上,当质量为m,带电荷量为+q的滑块以速度v沿斜面匀速下滑时,在此空间突然加上方向沿斜面向下的匀强电场E,且Eq=mg,滑块继续沿斜面滑动距离L到达斜面底端.则( )
如图所示,倾角为θ的绝缘斜面固定在水平面上,当质量为m,带电荷量为+q的滑块以速度v沿斜面匀速下滑时,在此空间突然加上方向沿斜面向下的匀强电场E,且Eq=mg,滑块继续沿斜面滑动距离L到达斜面底端.则( )| A. | 滑块到达斜面底端时的速度为$\sqrt{2gL}$ | |
| B. | 由于有摩擦,滑块下滑的加速度小于g | |
| C. | 在滑块加速下滑过程中,地面对斜面没有摩擦力 | |
| D. | 如果将电场方向改为竖直向下,滑块将加速下滑 |
15.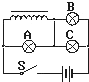 如图所示,自感线圈电阻很小(可忽略不及),自感系数很大,A、B、C是三只完全相同的灯泡,则S闭合后,以下说法正确的是( )
如图所示,自感线圈电阻很小(可忽略不及),自感系数很大,A、B、C是三只完全相同的灯泡,则S闭合后,以下说法正确的是( )
 如图所示,自感线圈电阻很小(可忽略不及),自感系数很大,A、B、C是三只完全相同的灯泡,则S闭合后,以下说法正确的是( )
如图所示,自感线圈电阻很小(可忽略不及),自感系数很大,A、B、C是三只完全相同的灯泡,则S闭合后,以下说法正确的是( )| A. | 闭合瞬间,三个灯都亮 | |
| B. | S闭合瞬间,A灯最亮,B和C灯的亮度相同 | |
| C. | S闭合后,过一会儿,A灯逐渐变暗,最后完全熄灭 | |
| D. | S闭合后过一会儿,B、C灯逐渐变亮,最后亮度相同 |
16.关于曲线运动下列说法中错误的是( )
| A. | 做曲线运动的物体,速度方向时刻改变,一定是变速运动 | |
| B. | 做曲线运动的物体,物体所受的合外力方向与速度的方向不在同一直线上,必有加速度 | |
| C. | 做曲线运动的物体不可能处于平衡状态 | |
| D. | 物体不受力或受到的合外力为零时,可能作曲线运动 |