题目内容
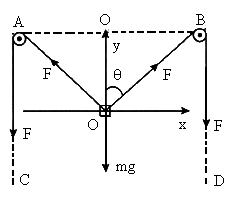
如图,轻质长绳水平地跨在相距2l的两个小定滑轮A、B上,质量为m的物块悬挂在绳上O点,O与A、B两滑轮的距离相等.在轻绳两端C、D分别施加竖直向下的恒力F=mg,先托住物块,使绳处于水平拉直状态,静止释放物块,在物块下落过程中,保持C、D两端的拉力F不变.
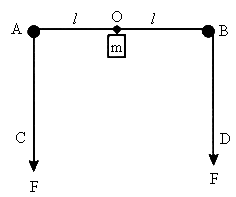
(1)当物块下落距离h为多大时,物块的加速度为零?
(2)在物块下落上述距离的过程中,克服C端恒力F做功W为多少?
(3)求物体下落过程中的最大速度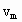 和最大距离H.
和最大距离H.
答案:略
解析:
解析:
|
(1)物块下落距离h为 (2)物块下落距离h过程中,克服C端恒力做功W为 (3)最大速度为 如图,(1)当物块所受合外力为零时,其加在速度为零.根据O点合力为0,应用正交分解方法可知
2F·cosθ=mg 解得 cosθ=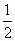 ,θ=60°, ,θ=60°,
所以物块此时下落的距离为
(2)在(1)中所给的过程中,C端上升距离为 所以克服 C端恒力F做功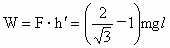
(3)根据动能定理
当 x=h时,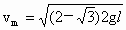
当 v=0时,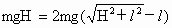
H= |

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
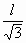 时,物块的加速度为0;
时,物块的加速度为0;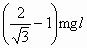 ;
;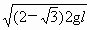 ,下落最大距离为
,下落最大距离为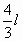 .
.

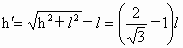
 .即拉力和重力对物块做的功等于物块动能的增量.当物块下落x时,依动能定理,有
.即拉力和重力对物块做的功等于物块动能的增量.当物块下落x时,依动能定理,有
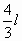
 (附加题)如图所示,轻质长绳水平地跨在相距为2L的两个小定滑轮A、B上,质量为m的物块悬挂在绳上O点,O与A、B两滑轮的距离相等.在轻绳两端C、D分别施加竖直向下的恒力F=mg.先托住物块,使绳处于水平拉直状态,由静止释放物块,在物块下落过程中,保持C、D两端的拉力F不变.
(附加题)如图所示,轻质长绳水平地跨在相距为2L的两个小定滑轮A、B上,质量为m的物块悬挂在绳上O点,O与A、B两滑轮的距离相等.在轻绳两端C、D分别施加竖直向下的恒力F=mg.先托住物块,使绳处于水平拉直状态,由静止释放物块,在物块下落过程中,保持C、D两端的拉力F不变.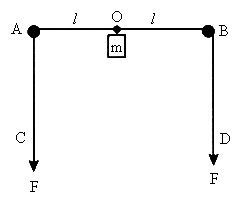
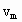 和最大距离H.
和最大距离H.
