题目内容
 (附加题)如图所示,轻质长绳水平地跨在相距为2L的两个小定滑轮A、B上,质量为m的物块悬挂在绳上O点,O与A、B两滑轮的距离相等.在轻绳两端C、D分别施加竖直向下的恒力F=mg.先托住物块,使绳处于水平拉直状态,由静止释放物块,在物块下落过程中,保持C、D两端的拉力F不变.
(附加题)如图所示,轻质长绳水平地跨在相距为2L的两个小定滑轮A、B上,质量为m的物块悬挂在绳上O点,O与A、B两滑轮的距离相等.在轻绳两端C、D分别施加竖直向下的恒力F=mg.先托住物块,使绳处于水平拉直状态,由静止释放物块,在物块下落过程中,保持C、D两端的拉力F不变.(1)当物块下落距离h为多大时,物块的加速度为零?
(2)在物块下落上述距离的过程中,克服C端恒力F做功W为多少?
(3)求物块下落过程中的最大速度Vm和最大距离H?
分析:由静止释放后,由于绳OC和绳OB对物块的合力小于重力,所以物块向下先作加速运动,随着物块的下落,两绳间的夹角逐渐减小.因为绳子对物块的拉力大小不变,恒等于F,所以随着两绳间的夹角减小,两绳对物块拉力的合力将逐渐增大,物块所受的合力逐渐减小,向下加速度逐渐减小.当物两绳的合力等于物块的重力时,即块的合外力为零时,速度达到最大值vm.故加速度为零时重力等于两绳的合力.之后,因为两绳间夹角继续减小,两绳合力大于物块的重力,物块所受合外力竖直向上,且逐渐增大,物块将作加速度逐渐增大的减速运动.当物块下降速度减为零时,物块竖直下落的距离达到最大值H.当物块的加速度为零时,由共点力平衡条件可求出相应的θ角,再由θ角求出相应的距离h,进而求出克服C端恒力F所做的功.对物块运用动能定理可求出物块下落过程中的最大速度Vm和最大距离H.
(1)故加速度为零时应有重力等于两绳的合力.
(2)由加速度为零时下落的高度h,可以由几何关系解出C点向上运动的距离,从而可以求出F做的功WF,故克服力F做的功为-WF
(3)由于下落h时速度为vm,故由动能定理即可求出vm;物块速度为零时下落距离为H,由动能定理求解H.
(1)故加速度为零时应有重力等于两绳的合力.
(2)由加速度为零时下落的高度h,可以由几何关系解出C点向上运动的距离,从而可以求出F做的功WF,故克服力F做的功为-WF
(3)由于下落h时速度为vm,故由动能定理即可求出vm;物块速度为零时下落距离为H,由动能定理求解H.
解答:解:(1)当物块所受的合外力为零时,加速度为零,此时物块下降距离为h.因为F恒定,所以两绳对物块拉力大小分别为F,两绳与竖直方向夹角均为θ,由平衡条件知:
2Fcosθ=mg2θ=120°,所以θ=60°,
由图知:h=Ltan30°=
L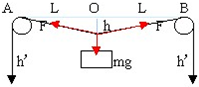 ①
①
(2)物块下落h时,绳的C、D端均上升h′由几何关系可得:h′=
-L ②
克服C端恒力F做的功为:W=Fh′③
由①②③式联立解得:W=(
-1)mgL
(3)在物块下落过程中,共有三个力对物块做功.重力做正功,两端绳子对物块的拉力做负功.两端绳子拉力做的功就等于作用在C、D端的恒力F所做的功.因为物块下降距离h时动能最大.由动能定理得:mgh-2W=
m
④
将①②③式代入④式解得:vm=
当物块速度减小为零时,物块下落距离达到最大值H,绳C、D上升的距离为H’.由动能定理得:
mgH-2mgH′=0,又H′=
-L,
联立解得:H=
l.
答:(1)当物块下落距离h为
时,物块的加速度为零.
(2)在物块下落上述距离的过程中,克服C端恒力F做功W为(
-1)mgL.
(3)物块下落过程中的最大速度vm为
,最大距离H为
l.
2Fcosθ=mg2θ=120°,所以θ=60°,
由图知:h=Ltan30°=
| ||
| 3 |
 ①
①(2)物块下落h时,绳的C、D端均上升h′由几何关系可得:h′=
| l2+h2 |
克服C端恒力F做的功为:W=Fh′③
由①②③式联立解得:W=(
2
| ||
| 3 |
(3)在物块下落过程中,共有三个力对物块做功.重力做正功,两端绳子对物块的拉力做负功.两端绳子拉力做的功就等于作用在C、D端的恒力F所做的功.因为物块下降距离h时动能最大.由动能定理得:mgh-2W=
| 1 |
| 2 |
| v | 2 m |
将①②③式代入④式解得:vm=
2(2-
|
当物块速度减小为零时,物块下落距离达到最大值H,绳C、D上升的距离为H’.由动能定理得:
mgH-2mgH′=0,又H′=
| H2+l2 |
联立解得:H=
| 4 |
| 3 |
答:(1)当物块下落距离h为
| ||
| 3 |
(2)在物块下落上述距离的过程中,克服C端恒力F做功W为(
2
| ||
| 3 |
(3)物块下落过程中的最大速度vm为
2(2-
|
| 4 |
| 3 |
点评:本题是连接体问题,根据牛顿第二定律研究加速度为零时的条件,由系统机械能守恒研究物块下降的最大距离,同时要合理运用几何关系辅助求解.

练习册系列答案
相关题目
 (附加题)如图所示,是一种测定风作用力的仪器原理图,P为金属球,悬挂在一细长金属丝下面,O是悬点,R0是保护电阻,CD是水平放置的光滑电阻丝,与细金属丝始终保持良好接触.无风时,金属丝与电阻丝在C点接触,此时A示数为I0;有风时金属丝将偏转一角度,角θ与风力大小有关,设风力方向水平向左,OC=h,CD=L,金属球质量为m,电阻丝单位长度的阻值为k,电源内电阻和金属丝电阻不计,金属丝偏角为θ时,A的示数为I′,此时风力为F,试写出:
(附加题)如图所示,是一种测定风作用力的仪器原理图,P为金属球,悬挂在一细长金属丝下面,O是悬点,R0是保护电阻,CD是水平放置的光滑电阻丝,与细金属丝始终保持良好接触.无风时,金属丝与电阻丝在C点接触,此时A示数为I0;有风时金属丝将偏转一角度,角θ与风力大小有关,设风力方向水平向左,OC=h,CD=L,金属球质量为m,电阻丝单位长度的阻值为k,电源内电阻和金属丝电阻不计,金属丝偏角为θ时,A的示数为I′,此时风力为F,试写出: (附加题)如图所示,倾角为α=60°的斜面上,放一质量为1kg大小可以忽略的物体,用劲度系数k=100N/m的弹簧平行于斜面吊着,物体放在PQ之间任何位置都能处于静止状态,而超过这一范围,物体都会沿斜面滑动.若AP=22cm,AQ=8cm,试求物体与斜面间的最大静摩擦力的大小.(g=10m/s2)
(附加题)如图所示,倾角为α=60°的斜面上,放一质量为1kg大小可以忽略的物体,用劲度系数k=100N/m的弹簧平行于斜面吊着,物体放在PQ之间任何位置都能处于静止状态,而超过这一范围,物体都会沿斜面滑动.若AP=22cm,AQ=8cm,试求物体与斜面间的最大静摩擦力的大小.(g=10m/s2) (附加题)如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场I和II,两电场的边界均是边长为L的正方形(不计电子所受重力).
(附加题)如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场I和II,两电场的边界均是边长为L的正方形(不计电子所受重力). 如图所示,以8m/s匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线18m.该车加速时最大加速度大小为2m/s2,减速时最大加速度大小为5m/s2.此路段允许行驶的最大速度为11.5m/s,下列说法中正确的有
如图所示,以8m/s匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线18m.该车加速时最大加速度大小为2m/s2,减速时最大加速度大小为5m/s2.此路段允许行驶的最大速度为11.5m/s,下列说法中正确的有