��Ŀ����
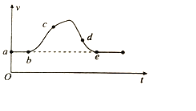
����Ŀ����ͼ����ʾ��һ����m=0.06kg�Ľ�������ֱ���������=37���ĵ����ϣ������ľ���l=0.2m���������뵼���Ķ�Ħ��������=0.8�����촦�ڴ�ֱ����ƽ�����µ��н���ǿ�ų��У��ų����±߽��������ƽ���Ҿ�������ľ���x=3m���Ÿ�Ӧǿ��B��ʱ��t�ı仯ͼ����ͼ����ʾ����֪t0ʱ�̽�������ʼ�˶���g=10m/s2��sin37��=0.6������R=3����������費�ƣ����Ħ�������ڻ���Ħ������
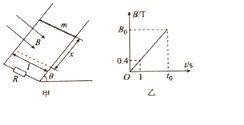
��1����B0��ֵ��
��2���ӽ�������ʼ�˶���t0ʱ���𣬸�������ʩ��һ���������ý�������v=0.1m/s���ٶ������»�����Ÿ�Ӧǿ��B��ʱ��t��ô�仯���ܱ�֤��������û�е�������д���������Ÿ�Ӧǿ��B��ʱ��t�仯�Ĺ�ϵʽ��
���𰸡���1��1.5T����2��B=![]() ��3.75s��t��33.75s����
��3.75s��t��33.75s����
��������
��1������ζ��ɿ�֪��·�в�����ʱ�뷽��ĸ�Ӧ�����������ֶ����֪�������ܵ���б�����µİ��������ɷ����ڵ�Ÿ�Ӧ���ɵã�E=![]() lx=0.4��0.2��3V=0.24V
lx=0.4��0.2��3V=0.24V
������I=![]() =
=![]() =0.08A
=0.08A
�Խ�������������������ͼ��ʾ��
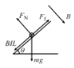
��������ʼ�˶�ʱ�У�mgsin��+B0Il=��mgcos��
������ã�B0=1.5T t0=![]() s=3.75s
s=3.75s
��2����������ʼ�˶�ʱB0=1.5T��Ҫ��֤��������û�е�����ֻҪ��֤�ų����±߽�ͽ�����Χ�ɵ������ڴ�ͨ����t0ʱ�̴�ͨ����ȣ�����
B0lx=Bl��x-v��t��
��t=t-t0
��ã�B=![]() ��3.75s��t��33.75s��
��3.75s��t��33.75s��