题目内容
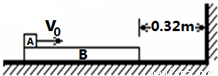
 在粗糙水平面上静置一长木板B,B的质量为M=2㎏,长度L=3m,B右端距竖直墙0.32m.现有一小物块 A,质量为m=1㎏,以v0=6m/s的速度从B左端水平地滑上B,如图所示.已知A、B间动摩擦因数为μ1=0.5,B与水平面间动摩擦因数为μ2=0.1,若B能与墙壁碰撞则立即停靠在墙边.取g=10m/s2.试分析小物块 A能否碰墙.
在粗糙水平面上静置一长木板B,B的质量为M=2㎏,长度L=3m,B右端距竖直墙0.32m.现有一小物块 A,质量为m=1㎏,以v0=6m/s的速度从B左端水平地滑上B,如图所示.已知A、B间动摩擦因数为μ1=0.5,B与水平面间动摩擦因数为μ2=0.1,若B能与墙壁碰撞则立即停靠在墙边.取g=10m/s2.试分析小物块 A能否碰墙.分析:分析两个物体的运动过程:B向右做匀加速运动,A向右做匀减速运动,根据牛顿第二定律求出它们的加速度.由运动学公式求出B碰墙所经历的时间,求出此时A的速度和对地位移.
分析A是否在B上.若仍在B上,B继续做匀减速运动,由运动学公式求出A的速度减为零时滑行的位移,判断能否撞墙.
分析A是否在B上.若仍在B上,B继续做匀减速运动,由运动学公式求出A的速度减为零时滑行的位移,判断能否撞墙.
解答:解:A的加速度a1=
=μ1g=5m/s2,方向向左
B的加速度a2=
=1m/s2,方向向右
设B经时间t1碰墙,
a2
=0.32m
解得:t1=0.8s
此时A的速度v1=v0-a1t1=2m/s>a2t1.
A相对B的位移x1=v0t1-
a1
-
a2
=2.88m<3m
因此A还在B上
此后B不动,A在B上以v1=2m/s的初速度做匀减速运动,直到停,所经位移为x2.
t2=
x2=v1t2-
a1
=0.4m>(3-2.88)m
因此A要跟墙发生碰撞.
答:小物块A能碰墙.
| μ1mg |
| m |
B的加速度a2=
| μ1mg-μ2(M+m)g |
| M |
设B经时间t1碰墙,
| 1 |
| 2 |
| t | 2 1 |
解得:t1=0.8s
此时A的速度v1=v0-a1t1=2m/s>a2t1.
A相对B的位移x1=v0t1-
| 1 |
| 2 |
| t | 2 1 |
| 1 |
| 2 |
| t | 2 1 |
因此A还在B上
此后B不动,A在B上以v1=2m/s的初速度做匀减速运动,直到停,所经位移为x2.
t2=
| v1 |
| a1 |
x2=v1t2-
| 1 |
| 2 |
| t | 2 2 |
因此A要跟墙发生碰撞.
答:小物块A能碰墙.
点评:本题的解题关键是运用牛顿第二定律分析物体的运动过程,边计算边判断.

练习册系列答案
相关题目
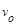 =6m/s的速度从B左端水平地滑上B,如图所示。已知A、B间动摩擦因数为μ1=0.5,B与水平面间动摩擦因数为μ2=0.1,若B能与墙壁碰撞则立即停靠在墙边。取g=10m/s2。试分析小物块 A能否碰墙。
=6m/s的速度从B左端水平地滑上B,如图所示。已知A、B间动摩擦因数为μ1=0.5,B与水平面间动摩擦因数为μ2=0.1,若B能与墙壁碰撞则立即停靠在墙边。取g=10m/s2。试分析小物块 A能否碰墙。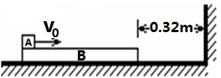
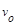 =6m/s的速度从B左端水平地滑上B,如图所示。已知A、B间动摩擦因数为μ1=0.5,B与水平面间动摩擦因数为μ2=0.1,若B能与墙壁碰撞则立即停靠在墙边。取g=10m/s2。试分析小物块 A能否碰墙。
=6m/s的速度从B左端水平地滑上B,如图所示。已知A、B间动摩擦因数为μ1=0.5,B与水平面间动摩擦因数为μ2=0.1,若B能与墙壁碰撞则立即停靠在墙边。取g=10m/s2。试分析小物块 A能否碰墙。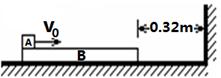
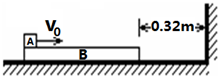 在粗糙水平面上静置一长木板B,B的质量为M=2㎏,长度L=3m,B右端距竖直墙0.32m.现有一小物块 A,质量为m=1㎏,以v0=6m/s的速度从B左端水平地滑上B,如图所示.已知A、B间动摩擦因数为μ1=0.5,B与水平面间动摩擦因数为μ2=0.1,若B能与墙壁碰撞则立即停靠在墙边.取g=10m/s2.试分析小物块 A能否碰墙.
在粗糙水平面上静置一长木板B,B的质量为M=2㎏,长度L=3m,B右端距竖直墙0.32m.现有一小物块 A,质量为m=1㎏,以v0=6m/s的速度从B左端水平地滑上B,如图所示.已知A、B间动摩擦因数为μ1=0.5,B与水平面间动摩擦因数为μ2=0.1,若B能与墙壁碰撞则立即停靠在墙边.取g=10m/s2.试分析小物块 A能否碰墙.