题目内容
已知地球和冥王星半径分别为r1、r2,绕太阳公转半径分别为r1′、r2′,公转线速度分别为v1′、v2′,表面重力加速度分别为g1、g2,平均密度分别为ρ1、ρ2,地球第一宇宙速度为v1,飞船贴近冥王星表面环绕线速度为v2,则下列关系正确的是( )
A、
| ||||||||
B、ρ1
| ||||||||
C、
| ||||||||
| D、g1 r12=g2r22 |
分析:根据万有引力提供向心力
=m
去求公转的线速度之比,以及第一宇宙速度之比.
根据万有引力等于重力求星球表面重力加速度之比.
| GMm |
| r2 |
| v2 |
| r |
根据万有引力等于重力求星球表面重力加速度之比.
解答:解:A、根据万有引力提供向心力:
=m
,v=
由于不知道地球和天王星的质量比,所以无法求出
,故A错误;
B、卫星的万有引力提供向心力,有:
G
=m
M=ρV
V=
πR3
联立得到:
=
(常数)
故:ρ1
=ρ2
,故B正确;
C、根据万有引力提供向心力:
=m
,解得:v=
地球和天王星的公转半径之比为r1′:r2′,所以公转速度之比
=
,故C正确;
D、星球表面的重力加速度g=
(其中r为星球的半径),可得gr2=GM,故g1r12=GM地,g2r22=GM冥,故g1r12≠g2r22,故D错误;
故选:BC.
| GMm |
| r2 |
| v2 |
| r |
|
由于不知道地球和天王星的质量比,所以无法求出
| v1 |
| v2 |
B、卫星的万有引力提供向心力,有:
G
| Mm |
| R2 |
| v2 |
| R |
M=ρV
V=
| 4 |
| 3 |
联立得到:
| ρR2 |
| v2 |
| 3 |
| 16π |
故:ρ1
| r | 2 1 |
| v | 2 2 |
| r | 2 2 |
| v | 2 1 |
C、根据万有引力提供向心力:
| GMm |
| r2 |
| v2 |
| r |
|
地球和天王星的公转半径之比为r1′:r2′,所以公转速度之比
| v1′ |
| v2′ |
|
D、星球表面的重力加速度g=
| GM |
| r 2 |
故选:BC.
点评:解决本题的关键搞清楚公转、第一宇宙速度等问题中,谁是中心天体,谁是环绕天体,然后根据万有引力提供向心力,万有引力等于重力进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 、
、 ,公转线速度分别为
,公转线速度分别为 、
、 ,表面重力加速度分别为g1、g2,平均密度分别为
,表面重力加速度分别为g1、g2,平均密度分别为 、
、 .地球第一宇宙速度为v1,飞船贴近冥王星表面环绕线速度为v2,则下列关系正确的是
.地球第一宇宙速度为v1,飞船贴近冥王星表面环绕线速度为v2,则下列关系正确的是  B.
B. C.
C. D.
D.
 、
、 ,公转线速度分别为
,公转线速度分别为 、
、 ,表面重力加速度分别为g1、g2,平均密度分别为
,表面重力加速度分别为g1、g2,平均密度分别为 、
、 .地球第一宇宵速度为v1,飞船贴近冥王星表面环绕线速度为v2,则下列关系正确的是 ( )
.地球第一宇宵速度为v1,飞船贴近冥王星表面环绕线速度为v2,则下列关系正确的是 ( )

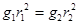
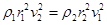
 、
、 ,公转线速度分别为
,公转线速度分别为 、
、 ,表面重力加速度分别为g1、g2,平均密度分别为
,表面重力加速度分别为g1、g2,平均密度分别为 、
、 .地球第一宇宙速度为v1,飞船贴近冥王星表面环绕线速度为v2,则下列关系正确的是
.地球第一宇宙速度为v1,飞船贴近冥王星表面环绕线速度为v2,则下列关系正确的是  B.
B. C.
C. D.
D.