题目内容
（2012?眉山模拟）已知地球和冥王星半径分别为r1、r2，公转半径分别为r1′、r2′，公转线速度分别为v1′、v2′，表面重力加速度分别为g1、g2，平均密度分别为ρ1、ρ2，地球第一宇宙速度为v1，飞船贴近冥王星表面环绕线速度为v2，则下列关系正确的是（ ）
分析：根据万有引力提供向心力
=m
去求公转的线速度之比，以及第一宇宙速度之比．
根据万有引力等于重力求星球表面重力加速度之比．
| GMm |
| r2 |
| v2 |
| r |
根据万有引力等于重力求星球表面重力加速度之比．
解答：解：A、根据万有引力提供向心力：
=m
v=
地球和天王星的公转半径之比为r1′：r2′，所以公转速度之比
=
故A正确；
B、根据万有引力提供向心力：
=m
，v=
由于不知道地球和天王星的质量比，所以无法求出
，故B错误．
C、重力加速度g=
（其中r′为公转半径），可得gr′2=GM日为定值，故g1r1′2=g2r2′2，故C错误．
D、根据星体密度公式ρ=
=
（其中T为星球表面卫星运行的周期，r为星球半径），故
为定值，故ρ1r12v22=ρ2r22v12，故D正确．
故选AD．
| GMm |
| r2 |
| v2 |
| r |
v=
|
地球和天王星的公转半径之比为r1′：r2′，所以公转速度之比
| v1′ |
| v2′ |
|
B、根据万有引力提供向心力：
| GMm |
| r2 |
| v2 |
| r |
|
由于不知道地球和天王星的质量比，所以无法求出
| v1 |
| v2 |
C、重力加速度g=
| GM日 |
| r′2 |
D、根据星体密度公式ρ=
| 3π |
| GT2 |
| 3v2 |
| 4Gπr2 |
| ρr2 |
| v2 |
故选AD．
点评：解决本题的关键搞清楚公转、第一宇宙速度等问题中，谁是中心天体，谁是环绕天体，然后根据万有引力提供向心力，万有引力等于重力进行求解．
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
（2012?眉山模拟）如图所示，质量分别为m和2m的A、B两个木块间用轻弹簧相连，放在光滑水平面上，A紧靠竖直墙．用水平力向左推B将弹簧压缩，推到一定位置静止时推力大小为F0，弹簧的弹性势能为E．在此位置突然撤去推力，下列说法中正确的是（ ）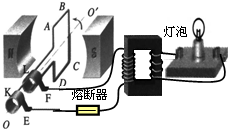
（2012?眉山模拟）如图所示，匝数为50匝的矩形闭合导线框ABCD处于磁感应强度大小B=