题目内容
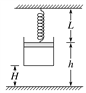
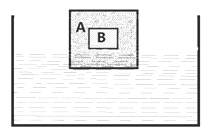
【题目】有一实心立方体A，边长为L，从内部去掉一部分物质，剩余部分质量为m，一立方体B 恰能完全填充A 的空心部分，质量也为m，如图所示，即B 的外表面与A 的内表面恰好接触。整体放在一个盛有密度为ρ的液体的容器里（容器无限大），刚开始，A 漂浮在液面上，用外力使A 向下产生位移b，平衡后由静止释放，A 将要上下振动（水的摩擦阻力不计）。可以证明该振动为简谐运动，振动过程中，A 始终不离开液面，也不被液面埋没，已知重力加速度g 求：
（1）试证明此振动为简谐振动。
（2）在最高点和最低点A 对B 的作用力。
【答案】（1）物体刚开始漂浮时：F浮=2mg，A向下产生位移b时，
，撤掉外力的瞬间，整体所受的合力：
， 
，所以为简谐振动。 （2）在最低点
，方向向上 ；在最高点
，方向向上
【解析】（1）物体刚开始漂浮时：F浮=2mg
A向下产生位移x时，
撤掉外力的瞬间，整体所受的合力：
所以为简谐振动。
（2）整体在最低点时，所受合外力F合＝ρgL2b
有牛顿第二定律可知整体的加速度
对B受力分析B受A向上的力F1
F1-mg=ma
解得F1＝mg+ma＝mg+
，方向向上
有对称性可知，在最高点B的加速度依然为a，方向向下，受A向上的作用力为F2
mg-F2=ma
解得F2＝mgma＝mg，方向向上
练习册系列答案
相关题目
