题目内容
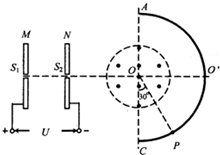如图所示，M、N是竖直正对放置的两个平行金属板，S1、S2是M、N板上的两个小孔；N板的右侧有一个在竖直面内，以O为圆心的圆形区域，该区域内存在垂直圆面向外的匀强磁场，另有一个同样以O为圆心的半圆形荧光屏AO’C；已知S1、S2、O和荧光屏的中间位置O’在同一直线上，且AC⊥S1O’．当在M、N板间加恒定电压U时，一带正电离子在S1处由静止开始加速向S2孔运动，最后打在图示的荧光屏上的P处，∠COP=30°．若要让上述带电离子（不计重力）仍在S1处静止开始加速，最后打在图示的荧光屏下边缘C处，求M、N板间所加电压的大小．分析：离子先在电场中加速，后进入磁场中做匀速圆周运动，由洛伦兹力充当向心力．当加速电压为U，离子打在图示的荧光屏上的P处，画出轨迹，由几何知识求出轨迹半径，由牛顿第二定律和动能定理得到电压U与半径、比荷、磁感应强度等量的关系式；当离子打在图示的荧光屏下边缘C处时，用同样的方法，求得加速电压．
解答：解：设离子的质量为m、电荷量为q，磁场的磁感应强度为B、所在区域的半径为R，离子加速后获得的速度为v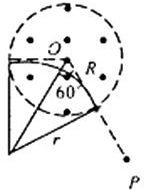
当电压为U时，由动能定理有 qU=
mv2 ①
在磁场中，离子做匀速圆周运动（见右图）
由牛顿第二定律可知 qvB=m
②
由①②式得 U=
③
其中，r=Rtan60°=
R ④
当电压为U′时，离子打在C处
同理有U′=
⑤
其中，r′=R ⑥
由③④⑤⑥可解得U′=
U
答：M、N板间所加电压的大小为
U．
当电压为U时，由动能定理有 qU=
| 1 |
| 2 |
在磁场中，离子做匀速圆周运动（见右图）
由牛顿第二定律可知 qvB=m
| v2 |
| r |
由①②式得 U=
| r2B2q |
| 2m |
其中，r=Rtan60°=
| 3 |
当电压为U′时，离子打在C处
同理有U′=
| r′2B2q |
| 2m |
其中，r′=R ⑥
由③④⑤⑥可解得U′=
| 1 |
| 3 |
答：M、N板间所加电压的大小为
| 1 |
| 3 |
点评：本题是常规题，由动能定理求离子加速获得的速度，画出轨迹．由几何知识求轨迹半径，都是常用的方法，要加强训练，熟练应用．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
如图所示，M、N是竖直放置的两平行金属板，分别带等量异种电荷，两极间产生一个水平向右的匀强电场，场强为E，一质量为m、电量为+q的微粒，以初速度v0竖直向上从两极正中间的A点射入匀强电场中，微粒垂直打到N极上的C点，已知AB=BC．不计空气阻力，则可知（ ）
如图所示，M、N是竖直放置的平行板电容器的两个极板，R0为定值电阻，R1、R2为可调电阻，用绝缘细线将质量为m、电荷量为+q的小球悬于电容器内部，闭合开关后，小球处于静止状态，现要使小球静止时细线与竖直方向的夹角变大（始终不与极板接触），正确操作的是（ ）
如图所示，M、N是竖直放置的两平行金属板，分别带等量异种电荷，两极板间产生一个水平向右的匀强电场，场强为E，一质量为m、电荷量为+q的微粒，以初速度v0竖直向上从两极正中间的A点射入匀强电场中，微粒垂直打到N极板上的C点，已知AB=BC．不计空气阻力，则可知（ ）| A、微粒在电场中做抛物线运动 | ||
| B、微粒打到C点时的速率与射入电场时的速率相等 | ||
C、MN板间的电势差为2m
| ||
D、MN板间的电势差为E
|
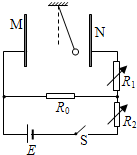如图所示，M、N是竖直放置的平行板电容器的两个极板，R0为定值电阻，R1、R2为可调电阻，用绝缘细线将质量为m、电荷量为+q的小球悬于电容器内部．闭合开关S，设法让小球做小角度摆动，测得周期为T．调节R1、R2，关于该摆做小角度振动的周期的判断，正确的是（小球摆动时不会碰极板）（ ）