题目内容
19. 如图所示,一电子沿Ox轴射入电场,在电场中的运动轨迹为OCD,已知$\overline{OA}$=$\overline{AB}$,电子过C、D两点时竖直方向的分速度为vCy和vDy;电子在OC段和OD动能变化量分别为△Ek1和△Ek2,则vCY:vDy=1:2;△Ek1:△Ek2=1:4.
如图所示,一电子沿Ox轴射入电场,在电场中的运动轨迹为OCD,已知$\overline{OA}$=$\overline{AB}$,电子过C、D两点时竖直方向的分速度为vCy和vDy;电子在OC段和OD动能变化量分别为△Ek1和△Ek2,则vCY:vDy=1:2;△Ek1:△Ek2=1:4.
分析 电子沿Ox轴射入匀强电场,做类平抛运动,水平方向做匀速直线运动,已知$\overline{OA}=\overline{AB}$,可知时间关系,竖直方向做匀加速运动,由运动学公式可分析速度关系,并能得到竖直位移的关系,由动能定理分析动能变化量的关系
解答 解:电子沿Ox轴射入匀强电场,做类平抛运动,水平方向做匀速直线运动,已知$\overline{OA}=\overline{AB}$,则电子从O到C与从C到D的时间相等.电子在竖直方向上做初速度为零的匀加速运动,则有vcy=atOC,vDy=atOD,所以 vcy:vDy=tOC:tOD=1:2.
根据匀变速直线运动的推论可知,在竖直方向上:yOC:yOD=1:4,
根据动能定理得
△Ek1=qEyOC,△Ek2=qEyOD,则得,△Ek1:△Ek2=1:4.
故答案为:1:2;1:4
点评 本题是类平抛运动问题,运用运动的分解法研究,灵活运用比例法求解,难度适中.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
4.一物体做直线运动的图象如图所示,则该物体( )


| A. | 先做匀加速运动,后做匀减速运动,速度方向相同 | |
| B. | 先做匀加速运动,后做匀减速运动,速度方向相反 | |
| C. | 先做匀减速运动,后做匀加速运动,速度方向相同 | |
| D. | 先做匀减速运动,后做匀加速运动,速度方向相反 |
8.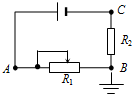 如图所示,电源电动势不变,内电阻不变,电路中B点接地,若滑动变阻器的滑片向右滑动时,A、C两点的电势的变化是( )
如图所示,电源电动势不变,内电阻不变,电路中B点接地,若滑动变阻器的滑片向右滑动时,A、C两点的电势的变化是( )
 如图所示,电源电动势不变,内电阻不变,电路中B点接地,若滑动变阻器的滑片向右滑动时,A、C两点的电势的变化是( )
如图所示,电源电动势不变,内电阻不变,电路中B点接地,若滑动变阻器的滑片向右滑动时,A、C两点的电势的变化是( )| A. | 两点的电势都升高 | B. | 两点的电势都降低 | ||
| C. | A点的电势升高,C点的电势降低 | D. | A点的电势降低,C点的电势升高 |
9.用欧姆表“×10”挡测量一个电阻的阻值,调零后测量时,发现指针的偏转角很小,下列说法中正确的是( )
| A. | 这个电阻值很小 | |
| B. | 这个电阻值很大 | |
| C. | 为了把电阻测量得更准确些,应换用“×1”挡,重新调零后再测量 | |
| D. | 为了把电阻测量得更准确些,应换用“×100”挡后直接测量 |
 如图所示,一定质量的气体温度保持不变,最初,U形管两臂中的水银相齐,烧瓶中气体体积为800mL;现用注射器向烧瓶中注入200mL水,稳定后两臂中水银面的高度差为25.3cm;已知76cm高的水银柱产生的压强约为1.0×105Pa,不计U形管中气体的体积.求:
如图所示,一定质量的气体温度保持不变,最初,U形管两臂中的水银相齐,烧瓶中气体体积为800mL;现用注射器向烧瓶中注入200mL水,稳定后两臂中水银面的高度差为25.3cm;已知76cm高的水银柱产生的压强约为1.0×105Pa,不计U形管中气体的体积.求: 如图所示,重20N的物体与竖直墙面间的动摩擦因数为0.1,当水平外力F为F1=100N时,物体与墙间的摩擦力是10N,当水平外力F为F2=400N时,物体与墙间的摩擦力是20N.
如图所示,重20N的物体与竖直墙面间的动摩擦因数为0.1,当水平外力F为F1=100N时,物体与墙间的摩擦力是10N,当水平外力F为F2=400N时,物体与墙间的摩擦力是20N. 在如图所示的电路中,S闭合时流过线圈L的电流是2A,流过灯泡A的电流是1A.将S突然断开,则S断开前后,能正确反映流过灯泡的电流I随时间t变化关系的是下图中的( )
在如图所示的电路中,S闭合时流过线圈L的电流是2A,流过灯泡A的电流是1A.将S突然断开,则S断开前后,能正确反映流过灯泡的电流I随时间t变化关系的是下图中的( )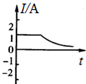



 半径为r、电阻为R的n匝圆形线圈在边长为l的正方形abcd外,匀强磁场充满并垂直穿过该正方形区域,如图甲所示.当磁场随时间的变化规律如图乙所示时,试求:
半径为r、电阻为R的n匝圆形线圈在边长为l的正方形abcd外,匀强磁场充满并垂直穿过该正方形区域,如图甲所示.当磁场随时间的变化规律如图乙所示时,试求: 如图所示,A、B两物体叠放在水平地面上,已知A、B的质量分别为mA、mB,A和B之间、B和地面之间的动摩擦因数均为μ.一轻绳一端系住物体A,另一端系于墙上,绳与竖直方向的夹角为θ.今欲用外力将物体B匀速向右拉出,求所加水平力F的大小.
如图所示,A、B两物体叠放在水平地面上,已知A、B的质量分别为mA、mB,A和B之间、B和地面之间的动摩擦因数均为μ.一轻绳一端系住物体A,另一端系于墙上,绳与竖直方向的夹角为θ.今欲用外力将物体B匀速向右拉出,求所加水平力F的大小.