题目内容
6. 如图所示,质量为m的物体在水平传送带上由静止释放,传送带由电动机带动,始终保持以速度v匀速运动,物体与传送带间的动摩擦因数为μ,物体在滑下传送带之前能保持与传送带相对静止,对于物体从静止释放到与传送带相对静止这一过程,下列说法中正确的是( )
如图所示,质量为m的物体在水平传送带上由静止释放,传送带由电动机带动,始终保持以速度v匀速运动,物体与传送带间的动摩擦因数为μ,物体在滑下传送带之前能保持与传送带相对静止,对于物体从静止释放到与传送带相对静止这一过程,下列说法中正确的是( )| A. | 摩擦生热Q=$\frac{1}{2}$mv2 | B. | 物体在传送带上的划痕长$\frac{{v}^{2}}{μg}$ | ||
| C. | 传送带克服摩擦力做的功为$\frac{1}{2}$mv2 | D. | 电动机增加的功率为μmgv |
分析 物体在传送带上运动时,物体和传送带要发生相对滑动,所以电动机多做的功一部分转化成了物体的动能另一部分就是增加了相同的内能.根据牛顿第二定律和运动学公式求出物体和传送带的位移,从而得出相对位移的大小.
解答 解:A、B、物体在传送带上的划痕长等于物体在传送带上的相对位移,物块达到速度v所需的时间$t=\frac{v}{μg}$,在这段时间内物块的位移${x}_{1}=\frac{{v}^{2}}{2μg}$,传送带的位移${x}_{2}=vt=\frac{{v}^{2}}{μg}$.则物体相对位移x=${x}_{2}-{x}_{1}=\frac{{v}^{2}}{2μg}$.
摩擦产生的热量:Q=$f{x}_{2}=μmg•\frac{{v}^{2}}{2μg}=\frac{1}{2}m{v}^{2}$.故A正确,B错误.
C、电动机多做的功转化成了物体的动能和内能,物体在这个过程中获得动能就是$\frac{1}{2}m{v}^{2}$,所以电动机多做的功一定要大于$\frac{1}{2}m{v}^{2}$.故C错误.
D、电动机增加的功率即为克服摩擦力做功的功率,大小为fv=μmgv,故D正确.
故选:AD.
点评 解决本题的关键知道物体在传送带上发生相对运动时的运动规律,以及知道能量的转化,知道电动机多做的功等于物体动能的增加和摩擦产生的内能之和.

练习册系列答案
相关题目
11.一定质量的理想气体发生状态变化时,其状态参量p、V、T的变化情况可能是( )
| A. | p、V、T都增大 | B. | p减小、V不变、T增大 | ||
| C. | p和T增大、V减小 | D. | p和V减小、T增大 |
15.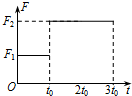 训练有素的杂技演员在进行“顶杆”表演时,用的是一根长直竹竿(假设竹竿质量不计),演员自杆顶由静止开始下滑,滑到杆底时速度正好为零.已知竹竿底部与下面顶杆人肩部之间有一压力传感器,传感器显示人的肩部受到竹竿底部施加的压力随时间变化情况如图所示,重力加速度为g.则( )
训练有素的杂技演员在进行“顶杆”表演时,用的是一根长直竹竿(假设竹竿质量不计),演员自杆顶由静止开始下滑,滑到杆底时速度正好为零.已知竹竿底部与下面顶杆人肩部之间有一压力传感器,传感器显示人的肩部受到竹竿底部施加的压力随时间变化情况如图所示,重力加速度为g.则( )
 训练有素的杂技演员在进行“顶杆”表演时,用的是一根长直竹竿(假设竹竿质量不计),演员自杆顶由静止开始下滑,滑到杆底时速度正好为零.已知竹竿底部与下面顶杆人肩部之间有一压力传感器,传感器显示人的肩部受到竹竿底部施加的压力随时间变化情况如图所示,重力加速度为g.则( )
训练有素的杂技演员在进行“顶杆”表演时,用的是一根长直竹竿(假设竹竿质量不计),演员自杆顶由静止开始下滑,滑到杆底时速度正好为零.已知竹竿底部与下面顶杆人肩部之间有一压力传感器,传感器显示人的肩部受到竹竿底部施加的压力随时间变化情况如图所示,重力加速度为g.则( )| A. | 从竹竿上滑下的演员的质量为$\frac{{F}_{1}+{F}_{2}}{2g}$ | |
| B. | 演员下滑过程中的加速度最大值为$\frac{{F}_{2}-{F}_{1}}{2{F}_{2}+{F}_{1}}$g | |
| C. | 演员下滑的速度最大值为$\frac{{F}_{2}-{F}_{1}}{2{F}_{2}+{F}_{1}}$gt0 | |
| D. | 竹竿的长度为$\frac{3({F}_{2}-{F}_{1})}{2{F}_{2}+{F}_{1}}$gt02 |
16.关于做曲线运动的物体的速度和加速度的以下说法中,正确的是( )
| A. | 速度的方向与大小一定都在时刻变化 | |
| B. | 速度的方向不断发生变化,速度的大小不一定发生变化 | |
| C. | 因为速度的方向不断改变,所以加速度的方向不断改变 | |
| D. | 因为速度的方向不断改变,所以加速度一定不为零,其方向与速度方向不共线 |
 如图,质量m=1kg的小球从A点由静止开始沿着光滑曲面轨道运动,已知A、B两点离水平面的高度h1=0.60米,h2=0.15米,g取10m/s2,问:
如图,质量m=1kg的小球从A点由静止开始沿着光滑曲面轨道运动,已知A、B两点离水平面的高度h1=0.60米,h2=0.15米,g取10m/s2,问: 甲、乙两个单摆的振动图线如图所示,根据振动图线可知甲、乙两单摆摆长之比是4:9;频率之比是3:2.
甲、乙两个单摆的振动图线如图所示,根据振动图线可知甲、乙两单摆摆长之比是4:9;频率之比是3:2.
 如图所示,光滑轨道NMAP固定在光滑的水平地面上,期中MAP为一半径为R的半圆弧轨道,相距为L的线段NM与半圆相切与M点,在圆的直径MP的右侧有场强大小为E,方向垂直MP向左的匀强电场;现从N点位置静止放开一个带电量为q质量为m的正电小球,求
如图所示,光滑轨道NMAP固定在光滑的水平地面上,期中MAP为一半径为R的半圆弧轨道,相距为L的线段NM与半圆相切与M点,在圆的直径MP的右侧有场强大小为E,方向垂直MP向左的匀强电场;现从N点位置静止放开一个带电量为q质量为m的正电小球,求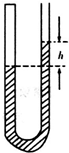 如图所示,一定质量的空气被水银封闭在静止于竖直平面的U形玻璃管内,U形管上端相平,左管封闭了L1=30m的空气柱,右管开口,管口离水银面L2=20cm,大气压P0=75cmHg,右管内水银面比左管内水银面高h=10cm,现从右侧管口处将一活塞缓慢向下推入管中,直到左右两侧水银面相平为止,整个过程温度不变,无漏气现象,求:
如图所示,一定质量的空气被水银封闭在静止于竖直平面的U形玻璃管内,U形管上端相平,左管封闭了L1=30m的空气柱,右管开口,管口离水银面L2=20cm,大气压P0=75cmHg,右管内水银面比左管内水银面高h=10cm,现从右侧管口处将一活塞缓慢向下推入管中,直到左右两侧水银面相平为止,整个过程温度不变,无漏气现象,求: