��Ŀ����
1�� ��ͼ��ʾ���⻬���NMAP�̶��ڹ⻬��ˮƽ�����ϣ�����MAPΪһ�뾶ΪR�İ�Բ����������ΪL���߶�NM���Բ������M�㣬��Բ��ֱ��MP���Ҳ��г�ǿ��СΪE������ֱMP�������ǿ�糡���ִ�N��λ�þ�ֹ�ſ�һ��������Ϊq����Ϊm������С����
��ͼ��ʾ���⻬���NMAP�̶��ڹ⻬��ˮƽ�����ϣ�����MAPΪһ�뾶ΪR�İ�Բ����������ΪL���߶�NM���Բ������M�㣬��Բ��ֱ��MP���Ҳ��г�ǿ��СΪE������ֱMP�������ǿ�糡���ִ�N��λ�þ�ֹ�ſ�һ��������Ϊq����Ϊm������С������1��С���˶���M��ʱ���ٶ�
��2��С���˶���A��ʱ��Բ�������С��ĵ���
��3��С���N��ſ����ٴλص�N�������ʱ�䣮
���� ��1��С���N���˶���M�㣬ֻ�е糡���������ɶ��ܶ������С���˶���M��ʱ���ٶȣ�
��2����M��A��С��������Բ���˶�����ţ�ٵڶ����ɺ���������ʽ�������С��ĵ�����
��3���ֶ���ʱ�䣮��N��M�����˶�ѧ��ʽ���ʱ�䣮��M��P����Բ���˶��Ĺ������ʱ�䣮��P���ң�С�����ȼ����˶������������ȼ����˶�����ţ�ٵڶ����ɺ��˶�ѧ��ʽ������ʱ�䣬�Ӷ��õ���ʱ�䣮
��� �⣺��1��С���N���˶���M�㣬�ɶ��ܶ�����
qEL=$\frac{1}{2}m{v}^{2}$
�ɵ�С���˶���M��ʱ���ٶ� v=$\sqrt{\frac{2qEL}{m}}$
��2����A�㣬��ţ�ٵڶ����ɵã�
ˮƽ�����У�Nx=m$\frac{{v}^{2}}{R}$
��ֱ�����У�Ny=mg
��С���˶���A��ʱ��Բ�������С��ĵ��� N=$\sqrt{{N}_{x}^{2}+{N}_{y}^{2}}$
������� N=$\sqrt{\frac{4{q}^{2}{E}^{2}{L}^{2}}{{R}^{2}}+{m}^{2}{g}^{2}}$
��3����N��M����L=$\frac{v}{2}{t}_{1}$�� t1=$\sqrt{\frac{2mL}{qE}}$
��M��P��t2=$\frac{��R}{v}$=��R$\sqrt{\frac{m}{2qEL}}$
��P���ң�С�����������ȼ����˶������������ȼ����˶�����ţ�ٵڶ����ɵ�
���ٶȴ�СΪ a=$\frac{qE}{m}$
�˶�ʱ��Ϊ t3=$\frac{v}{a}$=$\sqrt{\frac{2mL}{qE}}$
��С���N��ſ����ٴλص�N�������ʱ�� t=2��t1+t2+t3��=2��R$\sqrt{\frac{m}{2qEL}}$+4$\sqrt{\frac{2mL}{qE}}$
��
��1��С���˶���M��ʱ���ٶ���$\sqrt{\frac{2qEL}{m}}$��
��2��С���˶���A��ʱ��Բ�������С��ĵ�����$\sqrt{\frac{4{q}^{2}{E}^{2}{L}^{2}}{{R}^{2}}+{m}^{2}{g}^{2}}$��
��3��С���N��ſ����ٴλص�N�������ʱ���� 2��R$\sqrt{\frac{m}{2qEL}}$+4$\sqrt{\frac{2mL}{qE}}$��
���� ����Ĺؼ�Ҫ������С���˶����̵Ļ����ϣ�����ÿ�����̵��������ɣ��ر�Ҫע��С���˶���A��ʱ��Բ�������С��ĵ�������ˮƽ����������ֱ������ֻ����ˮƽ����

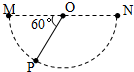 ��ͼ��ʾ��M��N��P��������MNΪֱ���ľ�Ե��Բ�⻬��ı�Ե�ϣ�O��Ϊ��Բ����Բ�ģ�MN�ڰ�Բ�����ˮƽֱ���ϣ���MOP=60�㣮�������Ϊq�ĵ��A����P�㣬�������Ϊm��������˵����ȷ���ǣ�������
��ͼ��ʾ��M��N��P��������MNΪֱ���ľ�Ե��Բ�⻬��ı�Ե�ϣ�O��Ϊ��Բ����Բ�ģ�MN�ڰ�Բ�����ˮƽֱ���ϣ���MOP=60�㣮�������Ϊq�ĵ��A����P�㣬�������Ϊm��������˵����ȷ���ǣ�������| A�� | ������M�����һ������B����ҪʹA��ɾ�ֹ����AB���һ�������ֵ�� | |
| B�� | ������N�����һ������B����ҪʹA��ɾ�ֹ����AB���һ����ͬ�ֵ�� | |
| C�� | ��ҪʹP��A��ɾ�ֹ����ʩ��һ����ǿ�糡����ǿһ��ΪE=$\frac{mg}{q}$ | |
| D�� | ��ҪʹP��A��ɾ�ֹ����P��ʩ�ӵĵ糡�ij�ǿ��СֵΪE=$\frac{mg}{2q}$ |
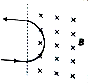 ��ͼ��ʾ��һ�����Ӻ�һ���������ش�ֱ�ڴŸ��߷����ͬһ������һ����ǿ�ų��У���֪ a���ӵ�����������������4��������������ӵ������2�����������ڴų��е��˶����켣���غϵģ��������ڴų��У�������
��ͼ��ʾ��һ�����Ӻ�һ���������ش�ֱ�ڴŸ��߷����ͬһ������һ����ǿ�ų��У���֪ a���ӵ�����������������4��������������ӵ������2�����������ڴų��е��˶����켣���غϵģ��������ڴų��У�������| A�� | �˶���ʱ����� | B�� | ���ٶȵĴ�С��� | ||
| C�� | �ٶȵĴ�С��� | D�� | ���ܵĴ�С��� |
 ��ͼ��ʾ������Ϊm��������ˮƽ���ʹ����ɾ�ֹ�ͷţ����ʹ��ɵ綯��������ʼ�ձ������ٶ�v�����˶��������봫�ʹ���Ķ�Ħ������Ϊ�̣������ڻ��´��ʹ�֮ǰ�ܱ����봫�ʹ���Ծ�ֹ����������Ӿ�ֹ�ͷŵ��봫�ʹ���Ծ�ֹ��һ���̣�����˵������ȷ���ǣ�������
��ͼ��ʾ������Ϊm��������ˮƽ���ʹ����ɾ�ֹ�ͷţ����ʹ��ɵ綯��������ʼ�ձ������ٶ�v�����˶��������봫�ʹ���Ķ�Ħ������Ϊ�̣������ڻ��´��ʹ�֮ǰ�ܱ����봫�ʹ���Ծ�ֹ����������Ӿ�ֹ�ͷŵ��봫�ʹ���Ծ�ֹ��һ���̣�����˵������ȷ���ǣ�������| A�� | Ħ������Q=$\frac{1}{2}$mv2 | B�� | �����ڴ��ʹ��ϵĻ��۳�$\frac{{v}^{2}}{��g}$ | ||
| C�� | ���ʹ��˷�Ħ�������Ĺ�Ϊ$\frac{1}{2}$mv2 | D�� | �綯�����ӵĹ���Ϊ��mgv |
 ��ͼ��ʾ�ĵ�·�У�RΪһ��ֵ���裬RTΪ�������裨�¶����ߣ������������ֵ��С�����������Ա�ѹ���������ѹU1���䣬���S�պϣ�����˵����ȷ���ǣ�������
��ͼ��ʾ�ĵ�·�У�RΪһ��ֵ���裬RTΪ�������裨�¶����ߣ������������ֵ��С�����������Ա�ѹ���������ѹU1���䣬���S�պϣ�����˵����ȷ���ǣ�������| A�� | RT����λ�õ��¶Ƚ���ʱ����L���� | |
| B�� | RT����λ�õ��¶Ƚ���ʱ����ѹ���������ѹ���� | |
| C�� | RT����λ�õ��¶Ƚ���ʱ����ѹ�������������С | |
| D�� | RT����λ�õ��¶Ƚ���ʱ����ѹ����������ʱ�� |

| A�� | ѡ��װ��1�о�ƽ��������ֱ���˶���Ӧ�����۾���A��B�����Ƿ�ͬʱ��� | |
| B�� | ѡ��װ��2Ҫ����ȶ���ϸˮ������ʾ��ƽ�켣����ֱ���϶�һ��Ҫ����ˮ�� | |
| C�� | ѡ��װ��3Ҫ��ø����ƽ�켣��ÿ�β�һ��Ҫ��б����ͬһλ���ɾ�ֹ�ͷ� | |
| D�� | ������װ���⣬Ҳ����ÿ��20֡��������������õ�������ƽ���˶��켣 |
 ��ͼ��ʾ���Ÿ�Ӧǿ�ȴ�С��ΪB����ǿ�ų��������ڱ߳�Ϊ2m�������η�Χ�ڣ����Ҹ�һ������ķ�Χ�ڣ��ų������෴����һ���߳�Ϊ1m�������ε��߿�abcd���ش�ֱ�Ÿ�Ӧ�������ٶ�v=1m/s����ͨ���ų�����ab�߽���ų�������
��ͼ��ʾ���Ÿ�Ӧǿ�ȴ�С��ΪB����ǿ�ų��������ڱ߳�Ϊ2m�������η�Χ�ڣ����Ҹ�һ������ķ�Χ�ڣ��ų������෴����һ���߳�Ϊ1m�������ε��߿�abcd���ش�ֱ�Ÿ�Ӧ�������ٶ�v=1m/s����ͨ���ų�����ab�߽���ų�������