��Ŀ����
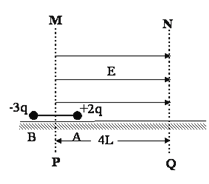
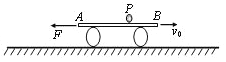
����Ŀ����ͼ��ʾ������ˮƽ���á����Ϊd�ij���������ڵ�ѹ�ɵ��ĵ�Դ�ϣ�����֮����Ҳ�������ڷ���ֱֽ���������ǿ�ų�������ī��ӡ������ڿ����ϰ��±��棬����������������������Ϊm��ˮƽ�ٶȾ�Ϊv0������ȵ������ī�Σ����ڵ�Դ��ѹ��U��ī���ڵ糡����ǡ����ˮƽ����������ֱ���˶�������糡���ų�������������մ�ֱ�����°��M�㣮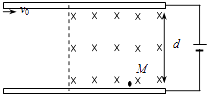
��1���ж�ī��������ɵ����࣬������������
��2����Ÿ�Ӧǿ��B��ֵ��
��3���ֱ�����ڷ��䣬ʹ����ֱ���Ƶ������м��λ�ã�Ϊ��ʹī�����ܵ����°�M�㣬Ӧ���Ÿ�Ӧǿ�ȵ���B�䣬��B��Ĵ�СΪ���٣�
���𰸡�
��1���⣺ī���ڵ糡����������ֱ���˶����У�q ![]() =mg����
=mg����
�ɢ�ʽ�ã�q= ![]() ����
����
���ڵ糡�������£�������ܵĵ糡���������ϣ���֪ī�δ�����ɣ�
��ī�δ����磬�����Ϊ ![]() ��
��
��2���⣺ī�δ�ֱ�����ų�����������������糡��ƽ�⣬�����������ṩ��������ī��������Բ���˶����У�
qv0B=m ![]() ����
����
����ī�ν���ų���ײ��ļ��ι�ϵ����֪ī���ڸ�����ǡ������ķ�֮һԲ���˶�����뾶R=d����
�ɢڢۢ�ʽ�ã�B= ![]() ����
����
�𣺴Ÿ�Ӧǿ��Ϊ ![]() ��
��
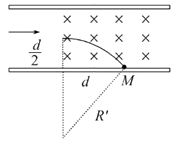
��3���⣺�������裬ī�ε��˶��켣��ͼ����Բ���˶��İ뾶ΪR�䣬�У�
qv0B��=m ![]() ����
����
��ͼʾ�ɵã�R��2=d2+��R�䩁 ![]() ��2����
��2����
�ã�R��= ![]() d����
d����
�����ڢޢ�ʽ�ɵã�B��= ![]() ��
��
��B��Ĵ�СΪ ![]() ��
��
����������1�����ݵ糡��������ƽ�����������Ĵ�С��ͨ���糡���ķ���ȷ����ɵ���������2��ī�δ�ֱ�����ų�����������������糡��ƽ�⣬����������Բ���˶����������Ӵ�ֱ����M�㣬ͨ�����ι�ϵ�ó����ӵĹ���뾶���������������ṩ����������Ÿ�Ӧǿ�ȵĴ�С����3�����ݼ��ι�ϵ�ó�������Բ���˶��Ĺ���뾶����ϴ��������ڴų����˶��İ뾶��ʽ����Ÿ�Ӧǿ�ȵĴ�С��

 ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д� �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�