题目内容
如图所示匀强电场E的区域内，在O点处放置一点电荷+Q， a、b、c、d、e、f为 以O点为球心的球面上的点，aecf平面与电场线平行，bedf平面与电场线垂直，则下列说法中正确的是（ ）
| A．b、d两点的电场强度相同 |
| B．a点的电势大于f点的电势 |
| C．点电荷+q在球面上任意两点之间移动时，电场力一定做功 |
| D．将点电荷+q在球面上任意两点之间移动，从球面上a点移动到c点的电势能变化量最大 |
BD
解析试题分析：空间任何一点的电场都是由匀强电场和点电荷的电场叠加面成，根据平行四边形定则分析各点场强关系，场强是矢量，只有大小和方向都相同时，场强才相同．根据叠加原理，判断各点的电势关系。若两点间电势差不为零，电场力做功不为零。点电荷+Q在b点产生的电场方向为竖直向上，在d点产生的电场方向为竖直向下，匀强电场方向水平向右，根据平行四边形定则可知，b点的合场强斜向右上方，d点的合场强斜向左下方，两点场强大小相同，方向不同，电场强度不同，故A错误；在匀强电场a、c两点有电势差，且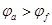
而在点电荷 电场中电场a、f两点电势相等，根据叠加原理可知，a点的电势大于f点的电势，B选项正确；匀强电场中bedf平面是个等势面，点电荷+Q产生的电场中bedf平面也是等势面，则叠加后bedf平面是等势面．在此面上移动电荷电场力不做功，故C错误；在匀强电场中ac两点的电势差最大，故在这两点间移动电荷，电场力做功最大，电势能变化最大，故D正确。本题关键是运用叠加原理分析两点间场强和电势的关系。
考点：电场叠加 电场力做功与电势能的关系
如图所示，在矩形ABCD的AD边和BC边的中点M和N各放一个点电荷，它们分别带等量的正、负电荷。E、F是AB边和CD边的中点，P、Q两点在MN的连线上，MP=QN．对于E、F、P、Q四点，其中电场强度相同、电势相等的两点是 （ ）
| A．E和F | B．P和Q | C．A和B | D．C和D |
如图电路中，C2 =2C1 ,R2=2R1，下列说法正确的（电源内阻不计）：（ ）
| A．开关处于断开状态，电容C2的电荷量等于C1的电荷量[ |
| B．开关处于断开状态，电容C1的电荷量大于C2的电荷量 |
| C．开关处于接通状态，电容C2的电荷量大于C1的电荷量 |
| D．开关处于接通状态，电容C1的电荷量等于C2的电荷量 |
在点电荷Q的电场中，一个电子通过时的轨迹如图实线所示，a、b为两个等势面，则下列判断中正确的是( )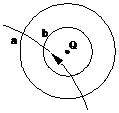
| A．Q一定为负电荷 |
| B．电子从b到a的过程中电场力做负功 |
| C．电子经过两等势面的动能Eka＞Ekb |
| D．电子在两等势面上的电势能Epa＞Epb |
带等量的同种正电的点电荷的连线和中垂线如图所示。现将一个带负电的试探电荷先从图中a点沿直线移到b点，再从b点沿直线移到c点，则试探电荷在这全过程中（ ）
| A．所受的电场力先做正功后做负功 |
| B．所受的电场力先做负功后做正功 |
| C．电势能一直增加 |
| D．电势能一直减小 |
如图所示，匀强电场中有a、b、c三点，在以它们为顶点的三角形中，∠a＝30°，∠c＝90°.电场方向与三角形所在平面平行．已知a、b和c点的电势分别为(2－
)V、(2＋)V和2 V．该三角形的外接圆上最低、最高电势分别为 ( ) 
| A．(2－)V、(2＋)V | B．0、4V |
C． V、 V | D．0、2V |
如图甲，真空中有一半径为R、电荷量为＋Q的均匀带电球体，以球心为坐标原点，沿半径方向建立x轴。理论分析表明，x 轴上各点的场强随x变化关系如图乙，已知x1与R两点间距大于R与x2的两点间距，则
A．x2处场强大小为 |
| B．x1、x2两点处的电势相同 |
| C．球内部的电场为匀强电场 |
| D．假设将试探电荷沿x轴移动，则从x1移到R处和从R移到x2处静电力做功相同 |
如图所示为匀强电场的电场强度E随时间t变化的图像．当t=0时，在此匀强电场中由静止释放一个带电粒子，设带电粒子只受电场力的作用，则下列说法中正确的是 ( )
| A．带电粒子将始终向同一个方向运动 |
| B．2s末带电粒子回到原出发点 |
| C．3s末带电粒子的速度不为零 |
| D．O～3s内，电场力做的总功为零 |