题目内容
6.甲车在前以v1=15m/s的速度匀速行驶,乙车在后以v2=9m/s的速度行驶.当两车相距L=32m时,甲车开始刹车,加速度大小为a=1m/s2.两车均视为质点.求:(1)甲车开始刹车到减速为零所花时间t0
(2)乙车追上甲车前二者距离的最大值d
(3)以甲车开始刹车时刻为计时起点,乙车追上甲车所花时间t(该结果用小数表示,且小数点后保留两位)
分析 (1)根据t=$\frac{△v}{a}$求解甲车刹车时间;
(2)当两车距离最大时,速度相等,根据运动学基本公式列式计算;
(3)乙车追上甲车时两车位移关系有:x甲+32=x乙列式计算可得结果.
解答 解:(1)甲车刹车时间为:
${t}_{0}=\frac{△v}{a}=\frac{0-15}{-1}=15s$
(2)两车距离最大时乙车的速度与甲车的速度相等,设此时甲车的速度为:v甲,即:
v甲=v乙
因为甲车做匀变速运动,则:
v甲=v甲0+at1
得:t1=$\frac{{v}_{甲}-{v}_{1}}{a}=\frac{9-15}{-1}=6s$
乙车前进的距离为:
x乙=v乙t1=9×6m=54m
甲车前进的距离为:
${x}_{甲}=\frac{{v}_{1}+{v}_{甲}}{2}{t}_{1}=\frac{9+15}{2}×6=72m$
所以两车的最大距离为:
△xm=L+x甲-x乙=32+72-54=50m
得:△xm=50m
(3)设经过时间t追上.依题意:
${v}_{1}t-\frac{1}{2}a{t}^{2}+L={v}_{2}t$
解得:t=16s和t=-4s(舍去)
显然,甲车停止后乙再追上甲.
甲车刹车的位移:
${x}_{甲}=\frac{{{v}_{0}}^{2}}{2a}=112.5m$
乙车的总位移:
x乙=x甲+32=144.5m
$t=\frac{{x}_{乙}}{{v}_{2}}=16.06s$
答:(1)甲车开始刹车到减速为零所花时间t0为15s;
(2)两车间相遇前的最大距离为50m;
(3)经16.06s乙车追上甲车.
点评 此题要注意:乙追上甲车可能有两种不同的情况:甲车停止前被追及和甲车停止后被追及.究竟是哪一种情况,应根据解答结果,有实际情况判断.
追及相遇问题一定要把握三个点:①速度相等时一般距离不是最大扭是最小;②位移关系;③时间关系..

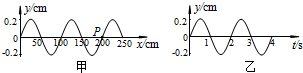
| A. | v=0.25m/s,向右传播 | B. | v=0.50m/s,向左传播 | ||
| C. | v=0.25m/s,向左传播 | D. | v=0.50m/s,向右传播 |
 两个轻弹簧分别与质量为m的物体相连接,劲度系数分别为k1和k2,装置呈竖直状态静止在水平地面上,如图所示.劲度系数为k2的弹簧与地面不栓接.现用竖直向上的拉力F拉劲度系数为k1的弹簧上端A点,使A点缓慢上升,当下边弹簧的下端即将离开地面时( )
两个轻弹簧分别与质量为m的物体相连接,劲度系数分别为k1和k2,装置呈竖直状态静止在水平地面上,如图所示.劲度系数为k2的弹簧与地面不栓接.现用竖直向上的拉力F拉劲度系数为k1的弹簧上端A点,使A点缓慢上升,当下边弹簧的下端即将离开地面时( )| A. | 物体比施加F前高$\frac{mg}{{k}_{2}}$ | B. | A点比施加F前高$\frac{mg}{{k}_{1}}$ | ||
| C. | F<mg | D. | F>mg |
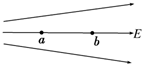 (多选)如图为某正电荷Q产生的电场线分布图,a、b是电场中的两点.将电荷量为q=5×10-8 C的正点电荷(试探电荷)置于a点,所受电场力为2×10-3 N,则下列判断正确的是( )
(多选)如图为某正电荷Q产生的电场线分布图,a、b是电场中的两点.将电荷量为q=5×10-8 C的正点电荷(试探电荷)置于a点,所受电场力为2×10-3 N,则下列判断正确的是( )| A. | 将电荷量为q的负点电荷放于a点,a点电场强度大小为4×104 N/C,方向向左 | |
| B. | a点的电场强度大小为4×104 N/C,方向向右 | |
| C. | 将点电荷q从a点移走,则该点的电场强度为零 | |
| D. | b点处的电场强度小于4×104 N/C |
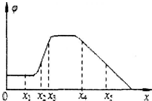
| A. | 空间各点场强的方向均与x轴垂直 | |
| B. | 电荷沿x轴从0移到x1的过程中,一定不受电场力的作用 | |
| C. | 正电荷沿x轴从x2移到x3的过程中,电场力做正功 | |
| D. | 负电荷沿x轴从x4移到x5的过程中,电场力做负功 |
| A. | 可能是向北 | B. | 可能是向南 | C. | 可能是竖直向上 | D. | 可能是竖直向下 |
 如图所示,光滑球重10N,球的半径20cm,绳的一端与球面上C点相连,AC的延长线经过圆心,使球靠在墙上而静止,绳子长20cm,求:
如图所示,光滑球重10N,球的半径20cm,绳的一端与球面上C点相连,AC的延长线经过圆心,使球靠在墙上而静止,绳子长20cm,求: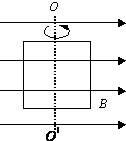 如图所示,把一个面积为8.0×10-2m2的单匝矩形线圈放在磁感应强度为2.0×10-2T的匀强磁场中,当线圈平面与磁场方向平行时,穿过线圈平面的磁通量为0Wb;在线圈绕OO′轴转动至与磁场方向垂直的过程中,穿过线圈平面的磁通量变大(填“大”或“小”)
如图所示,把一个面积为8.0×10-2m2的单匝矩形线圈放在磁感应强度为2.0×10-2T的匀强磁场中,当线圈平面与磁场方向平行时,穿过线圈平面的磁通量为0Wb;在线圈绕OO′轴转动至与磁场方向垂直的过程中,穿过线圈平面的磁通量变大(填“大”或“小”)