题目内容
【题目】如图甲所示,足够长的光滑平行金属导轨MN、PQ竖直放置,其宽度L=lm,—匀强磁场垂直穿过导轨平面,导轨的上端M与P之间连接一阻值为R=0.40Ω的电 阻,质量为m=0.01kg.电阻为r=0.30Ω的金属棒ab 紧贴在导轨上,现使金属棒ab由静止开始下滑,下滑过程中ab始终保持水平,且与导轨接触良好,其下滑距离x与时间t的关系如图乙所示,图象中的OA段为曲线,AB段为直线,导轨电阻不计,g取10m/s2(忽略ab棒运动过程中对原磁场的影响)。
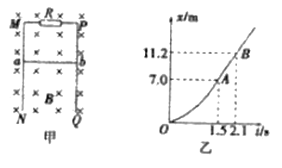
(1)判断金属棒两端a、b的电势高低;
(2)当t=1.5s时重力对金属棒ab做功的功率
(3)求磁感应强度B的大小;
(4)在金属棒ab从开始运动的1.5s内,电阻R上产生的热量。
【答案】(1)![]() (2)0.7W (3)B=0.1T (4)QR
(2)0.7W (3)B=0.1T (4)QR![]()
【解析】
(1)由右手定则判断出感应电流方向,然后判断电势高低。
(2)x-t图象中AB段为直线,说明从t=1.5s时开始金属棒ab做匀速直线运动,由图线的斜率求出速度v,由P=mgv求t=1.5s时重力对金属棒ab做功的功率。
(3)金属棒ab做匀速直线运动时,安培力与重力二力平衡,推导出安培力的表达式,根据平衡条件求出磁感应强度B的大小。
(4)根据能量守恒定律和焦耳定律求解金属棒ab在开始运动的1.5s内电路中产生的总热量,再求R上产生的热量。
(1)由右手定则判断![]() ;
;
(2)金属棒ab先做加速度减小的加速运动,t=1.5s后以速度vt匀速下落
由题图乙知![]()
由功率定义得t=1.5s时,重力对金属棒ab做功的功率:
PG=mgvt=0.01×10×7W=0.7W
(3)当金属棒匀速下落时,由共点力平衡条件得
mg=BIL ①
金属棒产生的感应电动势E=BLvt ②
则电路中的电流I=![]() ③
③
由图象可得vt=7m/s
代入数据解得B=0.1T
(4)在01.5s,以金属棒ab为研究对象,根据动能定理得
mgh-W安=![]() mvt2-0 ④
mvt2-0 ④
W安=0.455J
对闭合回路由闭合电路欧姆定律得:E电=I(R+r) ⑤
则电阻R两端的电压U为:UR=![]() ⑥
⑥
电阻R上产生的热量QR=![]()

 阅读快车系列答案
阅读快车系列答案