题目内容
【题目】如图所示，质量为M的小球被一根长为L的可绕O轴在竖直平面内自由转动的轻质杆固定在其端点，同时又通过轻绳跨过光滑定滑轮与质量为m的小球相连．不计摩擦，忽略杆水平时质量为M的小球与滑轮间的距离，竖直绳足够长，若将M由杆呈水平状态即由图示位置开始释放，则（ ）
A.m在运动过程中满足机械能守恒
B.当m与M的速度相同时，其速度的大小为 
C.在m上升的过程中绳对m的拉力大于m的重力
D.若M能通过最低点，则其速度大小为 
【答案】B,C,D
【解析】解：A、由于绳子拉力对m做功，所以m在运动过程中机械能不守恒，A不符合题意．
B、当系M的绳子与杆垂直时，m与M的速度相同时，设此时杆与水平方向的夹角为α，根据几何知识可得 cosα= 
=0.8，sinα=0.6
设M与m的速度大小为v．根据系统的机械能守得：MgLsinα=mg（ 
Lsinα﹣ 
L）+ 
，解得 v= 
．B符合题．
C、m加速上升，处于超重状态，则绳对m的拉力大于m的重力，C符合题意．
D、M能通过最低点时，设系M的绳与竖直方向的夹角为θ，则由几何知识可得 sinθ=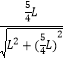 
= 
设此时M和m的速度分别为vM、vm，则vMsinθ=vm，
根据系统的机械能守恒得：MgL=mg（ 
﹣ L）+ 
MvM2+ mvm2；
解得 vM= 
．D符合题意．
所以答案是：BCD
【考点精析】利用机械能守恒及其条件和机械能综合应用对题目进行判断即可得到答案，需要熟知在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变；系统初态的总机械能E 1 等于末态的总机械能E 2 ，即E1 =E2；系统减少的总重力势能ΔE P减 等于系统增加的总动能ΔE K增 ，即ΔE P减 =ΔE K增；若系统只有A、
