题目内容
10.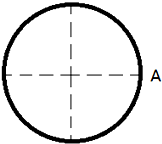 质点沿半径为d的圆形轨道运动,每2s移动$\frac{1}{4}$圆周,初始位置在某处的A点,如图所示,分别求出下列各种情况下的路程和位移的大小,并在图上标出各位移矢量的方向.
质点沿半径为d的圆形轨道运动,每2s移动$\frac{1}{4}$圆周,初始位置在某处的A点,如图所示,分别求出下列各种情况下的路程和位移的大小,并在图上标出各位移矢量的方向.(1)从A点开始到第2s末时;
(2)从A点开始到第4s末时;
(3)从A点开始到第8s末时.
分析 根据位移与路程的定义:路程等于物体运动轨迹的长度,位移的大小等于首末位置的距离.
解答 解:(1)从A点开始经过2s时间,移动了$\frac{1}{4}$圆周到达B点,如图所示:
路程为:$\frac{1}{2}πd$;位移为:$\sqrt{2}d$,方向A直线B;
(2)从A点开始经过4s时间,移动了$\frac{1}{2}$圆周到达C点,如图所示:
路程为:πd;位移为2d,方向:A指向C;
(3)从A点开始经过8s时间,移动了1个圆周又回到A点,则路程为:2πd,位移为零.
答:(1)从A点开始到第2s末时,路程为$\frac{1}{2}πd$,位移为$\sqrt{2}d$,方向A直线B;
(2)从A点开始到第4s末时,路程为$\frac{1}{2}πd$;位移为$\sqrt{2}d$,方向A直线B;
(3)从A点开始到第8s末时,路程为2πd,位移为零.
点评 解决本题的关键知道位移和路程的区别,知道位移的大小等于首末位置的距离.基础题目

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.物体以5m/s的速度匀速通过直线上的A、B两点,所用时间为2s,现在物体从A点由静止出发,先做匀加速直线运动(加速度为a1)到某一最大速度vm,然后立即做匀减速直线运动(加速度大小为a2)至B点速度恰好减为0,所用时间仍为2s.则物体的( )
| A. | vm只能为10m/s,与a1、a2的大小无关 | |
| B. | vm可为许多值,与a1、a2的大小有关 | |
| C. | a1、a2必须满足$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}=\frac{1}{5}$s2/m | |
| D. | a1、a2必须是一定的 |
1. 有一口井,水面距井口4m,现用水桶从井中提水(如图),水桶出井后又将其提升了1m.选井口处为坐标原点,以水桶竖直向上提升的路线为x轴,向上为正方向,则水桶在水面时的位置和最后的位置坐标分别是( )
有一口井,水面距井口4m,现用水桶从井中提水(如图),水桶出井后又将其提升了1m.选井口处为坐标原点,以水桶竖直向上提升的路线为x轴,向上为正方向,则水桶在水面时的位置和最后的位置坐标分别是( )
 有一口井,水面距井口4m,现用水桶从井中提水(如图),水桶出井后又将其提升了1m.选井口处为坐标原点,以水桶竖直向上提升的路线为x轴,向上为正方向,则水桶在水面时的位置和最后的位置坐标分别是( )
有一口井,水面距井口4m,现用水桶从井中提水(如图),水桶出井后又将其提升了1m.选井口处为坐标原点,以水桶竖直向上提升的路线为x轴,向上为正方向,则水桶在水面时的位置和最后的位置坐标分别是( )| A. | 4 m,1 m | B. | -4 m,1 m | C. | 5 m,0 | D. | -5 m,1 m |
15. 一对平行金属板AB水平放置接在一个如图的、电压恒定的电源上,两板间有一带电的粒子P恰好静止在两板之间,现把两板的距离增大,将发生下列哪种现象( )
一对平行金属板AB水平放置接在一个如图的、电压恒定的电源上,两板间有一带电的粒子P恰好静止在两板之间,现把两板的距离增大,将发生下列哪种现象( )
 一对平行金属板AB水平放置接在一个如图的、电压恒定的电源上,两板间有一带电的粒子P恰好静止在两板之间,现把两板的距离增大,将发生下列哪种现象( )
一对平行金属板AB水平放置接在一个如图的、电压恒定的电源上,两板间有一带电的粒子P恰好静止在两板之间,现把两板的距离增大,将发生下列哪种现象( )| A. | 电路中有逆时针方向的电流同时P向下运动 | |
| B. | 电路中有顺时针方向的电流同时P向下运动 | |
| C. | 电路中有逆时针方向的电流同时P向上运动 | |
| D. | 电路中有顺时针方向的电流同时P向上运动 |
19.下列关于近代物理知识的描述中,正确的是( )
| A. | 处于n=3能级状态的大量氢原子自发跃迁时,能发出3种种频率的光子 | |
| B. | β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 | |
| C. | 在${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+X核反应中,x是质子,这个反应过程叫α衰变 | |
| D. | 原子核所含核子单独存在时的总质量等于该原子核的质量 |
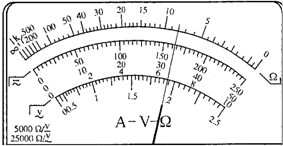 某一多用电表的欧姆挡有4挡,分别为×1Ω,×10Ω,×100Ω,×1000Ω,现用它来测某一未知电阻的阻值.当用×100Ω挡测量时,发现指针的偏转角度很小.为了使测量结果更准确,测量前应进行如下两项操作:先换用×1000挡(填“×10”或“×1000”),接着进行欧姆调零(填“机械调零”或“欧姆调零”),然后再进行测量并读数.下图为一正在测量中的多用电表表盘.
某一多用电表的欧姆挡有4挡,分别为×1Ω,×10Ω,×100Ω,×1000Ω,现用它来测某一未知电阻的阻值.当用×100Ω挡测量时,发现指针的偏转角度很小.为了使测量结果更准确,测量前应进行如下两项操作:先换用×1000挡(填“×10”或“×1000”),接着进行欧姆调零(填“机械调零”或“欧姆调零”),然后再进行测量并读数.下图为一正在测量中的多用电表表盘.