题目内容
3. 如图所示,竖直平面内有一直角坐标系,在y轴的右侧存在无限大的、场强大小为E、水平向左的匀强电场,在y轴的左侧同时存在一个垂直纸面向外、磁感应强度大小为B、水平宽度为a的匀强磁场.有一不计重力、带正电、比荷为$\frac{q}{m}$的粒子由+x轴上某一位置无初速度释放.
如图所示,竖直平面内有一直角坐标系,在y轴的右侧存在无限大的、场强大小为E、水平向左的匀强电场,在y轴的左侧同时存在一个垂直纸面向外、磁感应强度大小为B、水平宽度为a的匀强磁场.有一不计重力、带正电、比荷为$\frac{q}{m}$的粒子由+x轴上某一位置无初速度释放.(1)若其恰好经过磁场左边界上P点(-a,$\frac{a}{2}$),求粒子射出磁场Ⅰ的速度v1的大小;
(2)若其恰好经过y轴上的Q点(0,$\frac{a}{2}$),求粒子从释放开始第一次到达Q所用的时间.
分析 (1)根据牛顿第二定律,由洛伦兹力提供向心力,结合几何关系,即可求解;
(2)画出运动轨迹,粒子可能在磁场中经过半个圆周到Q点,也可能经过2个、3个、…、n个半圆到Q点,结合几何关系得到半径的通项,再根据牛顿第二定律列式求解.
解答 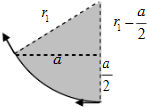 解:(1)如图所示,由几何关系可知:
解:(1)如图所示,由几何关系可知:
${r}_{1}^{2}$=a2+(r1-$\frac{a}{2}$)2;
可知,粒子在磁场中运动轨迹半径r1=$\frac{5a}{4}$;
由牛顿第二定律,可得:Bqv1=m$\frac{{v}_{1}^{2}}{{r}_{1}}$
因此射出磁场的速度v1=$\frac{5Bqa}{4m}$;
(2)粒子从释放开始到第一次到达Q点,可能轨迹如下图所示,
由几何关系,有:n•2r2=$\frac{a}{2}$,其中n=1,2,3,… 故r2=$\frac{a}{4n}$
故r2=$\frac{a}{4n}$
粒子在磁场中${r}_{2}=\frac{m{v}_{2}}{qB}$,T=$\frac{2πm}{qB}$
粒子在电场中匀加速直线运动${v}_{2}=\frac{Eq}{m}{t}_{1}$,
解得:${t}_{1}=\frac{Ba}{4nE}$
粒子在磁场中做匀速圆周运动,通过一个半圆的时间为$\frac{T}{2}$
从释放开始一直第一次到达Q所用的时间$t=(2n-1){t}_{1}+n\frac{T}{2}$
解得:t=n$\frac{πm}{Bq}+\frac{(2n-1)Ba}{4nE}$ 其中n=1,2,3,…
答:(1)若其恰好经过磁场左边界上P点(-a,$\frac{a}{2}$),粒子射出磁场Ⅰ的速度v1的大小为$\frac{5Bqa}{4m}$;
(2)若其恰好经过y轴上的Q点(0,$\frac{a}{2}$),粒子从释放开始第一次到达Q所用的时间为t=n$\frac{πm}{Bq}+\frac{(2n-1)Ba}{4nE}$ 其中n=1,2,3,….
点评 本题关键是明确粒子在电场和磁场中的受力情况和运动情况,画出运动轨迹,找出半径,注意第二问要考虑多解.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 一位同学在使用打点计时器时,纸带上的点不是圆点而是一些短线,如图所示,这可能的原因是( )
一位同学在使用打点计时器时,纸带上的点不是圆点而是一些短线,如图所示,这可能的原因是( )| A. | 接到了直流电源上 | B. | 电源电压不稳定 | ||
| C. | 电源频率不稳定 | D. | 打点针压得过紧 |
 伽利略为了研究自由落体运动的规律,将落体实验转化为著名的“斜面实验”,如图所示,对于这个研究过程,下列说法正确的是( )
伽利略为了研究自由落体运动的规律,将落体实验转化为著名的“斜面实验”,如图所示,对于这个研究过程,下列说法正确的是( )| A. | 亚里士多德首先建立了平均速度、瞬时速度、加速度等概念 | |
| B. | 斜面实验“冲淡”了重力的作用,便于小球运动时间的测量 | |
| C. | 伽利略用实验验证V与t成正比的最大困难是当时没有测量时间的仪器 | |
| D. | 伽利略科学思想方法的核心是把实验和逻辑推理和谐地结合起来 |
| A. | 加速度不变 | B. | 速度逐渐减小 | C. | 加速度逐渐增大 | D. | 速度逐渐增大 |
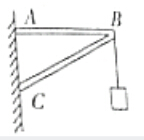 如图所示,在轻质的三角架上的B点细绳悬挂一个重为G的物体,则水平横梁受到的是拉力,斜梁BC受到的是压力作用.(填“拉”或“压”)
如图所示,在轻质的三角架上的B点细绳悬挂一个重为G的物体,则水平横梁受到的是拉力,斜梁BC受到的是压力作用.(填“拉”或“压”) 水平放置的平行金属板相距为d,板间有垂直纸面向里的匀强磁场,磁感应强度为B,极板按如图所示的方式接入电路.已知电源内阻为r,滑动变阻器的总阻值为R,滑片P的位置位于变阻器的中点.有一个质量为m、电荷量为+q的带电粒子,从两板中间左端沿中心线水平射入场区.不计粒子重力.
水平放置的平行金属板相距为d,板间有垂直纸面向里的匀强磁场,磁感应强度为B,极板按如图所示的方式接入电路.已知电源内阻为r,滑动变阻器的总阻值为R,滑片P的位置位于变阻器的中点.有一个质量为m、电荷量为+q的带电粒子,从两板中间左端沿中心线水平射入场区.不计粒子重力.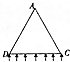 如图所示,在边长为a的等边三角形ACD区域内,存在垂直于所在平面向里的匀强磁场,大量的质量为m、电荷量为q的带正电粒子以相同速度沿垂直于CD的方向射入磁场,经磁场偏转后垂直于AD边射出的粒子在磁场中运动的时间为t0,不计粒子的重力及粒子间的相互作用.求:
如图所示,在边长为a的等边三角形ACD区域内,存在垂直于所在平面向里的匀强磁场,大量的质量为m、电荷量为q的带正电粒子以相同速度沿垂直于CD的方向射入磁场,经磁场偏转后垂直于AD边射出的粒子在磁场中运动的时间为t0,不计粒子的重力及粒子间的相互作用.求: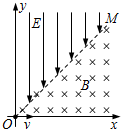 在如图所示的竖直平面直角坐标系xOy中,虚线OM与x轴成45°角.在OM与x轴之间(包括x轴)的区域存在垂直于坐标平面向里、磁感应强度大小为B的匀强磁场.在OM与y轴之间(包括y轴)的区域,存在沿y轴负方向的匀强电场(但电场强度大小未知).有一个质量为m、电荷量为q的带正电的粒子,以速度v沿x轴正方向从坐标原点O射入磁场区域并发生偏转,不计带电粒子的重力和空气阻力,粒子第二次进入电场后恰好运动到O点并从此离开电场和磁场.求:
在如图所示的竖直平面直角坐标系xOy中,虚线OM与x轴成45°角.在OM与x轴之间(包括x轴)的区域存在垂直于坐标平面向里、磁感应强度大小为B的匀强磁场.在OM与y轴之间(包括y轴)的区域,存在沿y轴负方向的匀强电场(但电场强度大小未知).有一个质量为m、电荷量为q的带正电的粒子,以速度v沿x轴正方向从坐标原点O射入磁场区域并发生偏转,不计带电粒子的重力和空气阻力,粒子第二次进入电场后恰好运动到O点并从此离开电场和磁场.求: