��Ŀ����
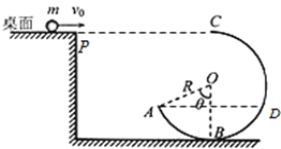
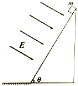
����Ŀ����ͼ��ʾ����ΪL���ڱڹ⻬��ֱ����ˮƽ�����30��ǹ̶����ã���һ����Ϊm��С��̶��ڹܵף���һ���ʹ⻬ϸ�߽�С��������ΪM=km��С���������С��������ڹܿڣ��ֽ�С���ͷţ�һ��ʱ���С�����ؾ�ֹ������С����������˶���ͨ���ܿڵ�ת��װ�ú���ƽ���˶���С����ת����������ʲ��䣮���������ٶ�Ϊg��
��1����С�����������еļ��ٶȴ�С��
��2����С��ӹܿ��׳�ʱ���ٶȴ�С��

���𰸡���1��С�����������еļ��ٶȴ�СΪ![]() ��
��
��2��С��ӹܿ��׳�ʱ���ٶȴ�С![]() ��K��2
��K��2
��������
���ʼʱС����б���������ȼ��٣�С�������Ҳ���ȼ��٣����ߵļ��ٶȴ�С��ȣ��Ը�����������������ţ�ٵڶ������г���ʽ��������̣�
С�����ؾ�ֹ������С������������ȼ����˶���������������������ţ�ٵڶ����ɽ����ʱ�ļ��ٶȣ���ǰһ�μ��ٶȲ��ȣ�������˶�ѧ��ʽ���С��ӹܿ��׳�ʱ���ٶȴ�С��
�⣺��1����ϸ���е�����ΪT����С���С����������
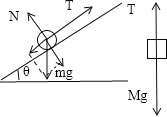
����ţ�ٵڶ����ɵã�
��M��Mg��T=Ma
��m��T��mgsin30��=ma
��M=km
��ã�a=![]()
��2����M���ʱ���ٶȴ�СΪv��m����ܿ�ʱ�ٶȴ�СΪv0��M��غ�m�ļ��ٶ�Ϊa0��
����ţ�ٵڶ������У�mgsin30��=ma0
����m�ȼ���ֱ���˶��У�v2=2aLsin30��
����С�����ؾ�ֹ������С��m�����������ȼ����˶��У�v2��v02=2a0L��1��sin30�㣩
��ã�v0=![]() ��k��2��
��k��2��
�𣺣�1��С�����������еļ��ٶȴ�СΪ![]() ��
��
��2��С��ӹܿ��׳�ʱ���ٶȴ�С![]() ��K��2
��K��2