题目内容
科技活动小组成员利用暑假进行社会实践活动时，发现可以利用古代抛石机的模型来验证机械能守恒定律，其原理如图所示．图中O为转轴，A球固定于杆上且质量为mA，B球放在勺形槽内且质量为mB.由静止释放轻杆后，可以逆时针转动，轻杆转到竖直位置时，B球被水平抛出．
(1)要验证机械能守恒定律，首先需要测量mA、mB及两球距O点的距离LA、LB，除此之外还需要测量的物理量有________．
A．A球从释放运动到最低点的时间t
B．O离地面的高度h
C．B球落地点与O的水平距离x
D．释放轻杆时A球的高度h0
(2)下列减小实验误差的措施中，可行的有________．
A．开始释放时，让轻杆水平
B．支架处地面与B球落地处地面要在同一水平面上
C．杆的硬度尽量高
D．在同一高度多次释放A球的前提下，取B球的平均落点，然后测量x
E．尽量减小转轴O处的摩擦力
F．尽量减小B球的质量
(3)在轻杆从水平状态无初速释放的前提下，结合上述测定的物理量，可求系统重力势能减少量为________，动能增加量为________，正常情况下会出现前者________(填“大于”或“小于”)后者．
（1）BCD（2）ABCDE（3）(mALA－mBLB)g 、
、大于；
解析试题分析：（1）验证实验中A 、B两球系统的机械能守恒，应先找出A、B两球初、始状态对应的机械能，与轻杆转动时间无关，所以B、C、D三项正确。（2）A项满足h0=h,B项可以保证测量操作容易控制，且便于计算重力势能的变化量，C项避免弹性势能的参与，D项是多次测量求平均值，E项减小摩擦力进而减少机械能向内能的转化，F项中B球应当尽量选用密度大的，以减小空气阻力，而与质量无关，所以ABCDE均正确。（3）轻杆从水平状态无初速释放，转到竖直位置过程中，A球重力做正功，B球重力做负功，且B球脱离勺形槽后做平抛运动，所以系统势能的减少量为(mALA－mBLB)g，动能的增加量为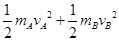
,
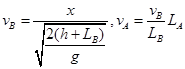,联立求解得动能的增加量为，因为有阻力，所以势能减小量一般大于动能增加量。
考点：机械能守恒
点评：需要对机械能守恒的条件，意义有深刻的认识，并且考虑到有机械能的损失而转化为内能。
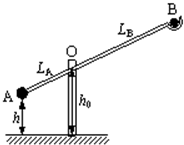科技活动小组成员利用暑假进行社会实践活动时，发现可以利用古代抛石机的模型验证系统机械能守恒定律，如图所示，一轻杆可绕固定于水平地面的竖直支架上的转动轴O转动，轻杆左端固定一小球A，轻杆右端的勺形槽内放置另一小球B．当将轻杆由图示位置静止释放后，A球向下运动可带动轻杆逆时针转动，直到轻杆到达竖直位置时，B球被水平抛出．要验证机械能守恒，首先要测得小球A、B的质量分别为mA、mB，以及A、B的球心离O的距离分别为LA、LB，除此之外还需要测量的物理量有（ ）