��Ŀ����
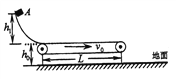
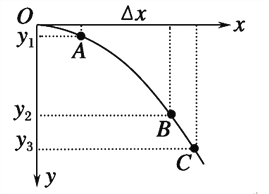
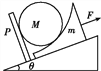
����Ŀ����ͼ��ʾ������ֱƽ���ڽ���ֱ������ϵxOy����ƽ������AM��BM��CM�����⻬�̶����������A��C���㴦��ͬһ��Բ�ϣ�C��Բ������һ�㣬A��M�ֱ�Ϊ��Բ��y��x����е㡣B����y�����ҡ�BMO��60����O��ΪԲ�ġ��ֽ�a��b��c����С��ֱ��A��B��C��ͬʱ�ɾ�ֹ�ͷţ����ǽ��ع���˶���M�㣬������ʱ��ֱ�ΪtA��tB��tC����tA��tB��tC��С��ϵ��(����)

A. tA��tC��tB
B. tA��tC��tB
C. tA��tC��tB
D. ����C���λ�ò�ȷ�������Ƚ�ʱ���С��ϵ
���𰸡�B
������������AM�Σ�λ��x1��![]() R�����ٶ�
R�����ٶ�![]() ������x��
������x��![]() at2�ã�
at2�ã� 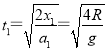 ������BM�Σ�λ��x2=2R�����ٶ�a2��gsin60����
������BM�Σ�λ��x2=2R�����ٶ�a2��gsin60����![]() g����x2��
g����x2��![]() at2�ã�
at2�ã� 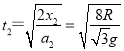 ������CM�Σ���CM����ֱ����н�Ϊ����ͬ���ɽ��
������CM�Σ���CM����ֱ����н�Ϊ����ͬ���ɽ��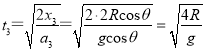 ����ѡB��
����ѡB��

��ϰ��ϵ�д�
 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д�
�����Ŀ