题目内容
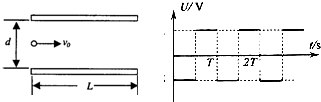
如图所示,质量和电量分别为m、e的带电粒子在t=0时,以初速度V0射入两平行极板之间,所加的电压大小为U0,方向按如图所示的规律变化,极板长为L,两板间的距离为d,要使粒子平行极板射出电场,则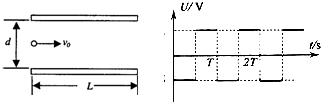
(1)交变电压的周期T满足什么条件;
(2)若带电粒子刚好从极板右边缘射出,电压U0满足什么条件.

(1)交变电压的周期T满足什么条件;
(2)若带电粒子刚好从极板右边缘射出,电压U0满足什么条件.
分析:(1)带电粒子在周期性电场作用下,做类平抛运动,竖直方向交替做匀加速运动和匀减速运动,水平方向做匀速直线运动,当要使粒子平行极板射出电场,加速和减速时间相等,分析得到时间与周期的关系,求出周期.
(2)若带电粒子刚好从极板右边缘射出,竖直方向位移之和等于
,由牛顿第二定律求出加速度,由位移公式求出每个
时间内竖直方向的位移大小y1,根据带电粒子刚好从极板右边缘射出,得到
=2ny1,联立解得电压U0满足的条件.
(2)若带电粒子刚好从极板右边缘射出,竖直方向位移之和等于
| d |
| 2 |
| T |
| 2 |
| d |
| 2 |
解答:解:(1)要使粒子平行极板方向射出电场,在电场中运动时间满足:
t=nT (n=1、2、3…)
带电粒子在水平方向上,做匀速直线运动,则
L=v0t
由以上两式得:T=
(n=1、2、3…)
(2)在0-
时间内,垂直极板方向通过的位移为
y1=
a(
)2
又a=
粒子刚好从右板边缘,则:
=2ny1
由以上各式得 U0=
(n=1、2、3…)
答:
(1)交变电压的周期T满足的条件是T=
(n=1、2、3…);
(2)若带电粒子刚好从极板右边缘射出,电压U0满足的条件是U0=
(n=1、2、3…).
t=nT (n=1、2、3…)
带电粒子在水平方向上,做匀速直线运动,则
L=v0t
由以上两式得:T=
| L |
| nv0 |
(2)在0-
| T |
| 2 |
y1=
| 1 |
| 2 |
| T |
| 2 |
又a=
| eU0 |
| md |
粒子刚好从右板边缘,则:
| d |
| 2 |
由以上各式得 U0=
2nmd2
| ||
| eL2 |
答:
(1)交变电压的周期T满足的条件是T=
| L |
| nv0 |
(2)若带电粒子刚好从极板右边缘射出,电压U0满足的条件是U0=
2nmd2
| ||
| eL2 |
点评:本题中带电粒子在周期性变化的电场运动,要抓住粒子运动的周期性,列出周期的通项,考查运用数学方法解决物理问题的能力.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 如图所示,质量为m,电量为q的小球以某一速度与水平成45°角进入匀强电场和匀强磁场,若微粒在复合场中做直线运动,则粒子带
如图所示,质量为m,电量为q的小球以某一速度与水平成45°角进入匀强电场和匀强磁场,若微粒在复合场中做直线运动,则粒子带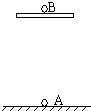 如图所示,A和B是两个带电小球,电量均为q,A固定在绝缘架上,B放在它的正上方很远距离的一块绝缘板上,现手持绝缘板使B从静止起以加速度a(a<g)竖直向下做匀加速运动.已知B的质量为m,静电力常量为k,空气阻力不计,求:
如图所示,A和B是两个带电小球,电量均为q,A固定在绝缘架上,B放在它的正上方很远距离的一块绝缘板上,现手持绝缘板使B从静止起以加速度a(a<g)竖直向下做匀加速运动.已知B的质量为m,静电力常量为k,空气阻力不计,求: