题目内容
【题目】如图中虚线MN是一垂直纸面的平面与纸面的交线,在平面右侧的半空间存在一磁感应强度为B的匀强磁场,方向垂直纸面向外.O是MN上的一点,从O点可以向磁场区域发射电量为+q、质量为m、速率为V的粒子,粒子射人磁场时的速度可在纸面内各个方向,已知先后射入两个粒子恰好在磁场中给定的P点相遇,P到O的距离为L.不计重力及粒子间的相互作用。

(1)所考察的粒子在磁场中的轨道半径.
(2)求这两个粒子从O点射人磁场的时间间隔.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设粒子在磁场中做圆周运动的轨道半径为R,由牛顿第二定律,有:qvB=m![]()
得:![]()
(2)如图所示,以OP为弦可画两个半径半径相同的圆,分别表示在P点相遇的两个粒子的轨道,圆心和直径分别为O1、O2和OO1Q1、OO2Q2,在O处两个圆的切线分别表示两个粒子的射入方向,用θ表示它们之间的夹角.由几何关系可知:∠PO1Q1=∠PO2Q2=θ
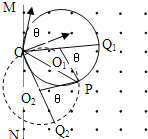
从O点射入到相遇,粒子1的路程为半个圆周加弧长Q1P
Q1P=Rθ
粒子2的路程为半个圆周减弧长PQ2
PQ2=Rθ
粒子1运动的时间:t1=![]()
粒子2运动的时间: t2=![]()
两粒子射入的时间间隔:△t=t1t2=![]()
因Rcos![]() θ=
θ=![]() L
L
得θ=2arccos![]()
解得:△t=![]()

练习册系列答案
相关题目