Question

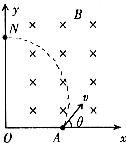（2011?南昌模拟）如图所示，有界匀强磁场的磁感应强度为B，区域足够大，方向垂直于纸面向里，直角坐标系xoy的y轴为磁场的左边界，A为固定在x轴上的一个放射源，内装镭核（

226 88

Ra）沿着与+x成θ角方向释放一个a粒子后衰变成氡核（Rn）．a粒子在y轴上的N点沿-x方向飞离磁场，N点到O点的距离为l，已知OA间距离为

l

2

，a粒子质量为m，电荷量为q，氡核的质量为m₀．
（1）写出镭核的衰变方程；
（2）如果镭核衰变时释放的能量全部变为a粒子和氡核的动能，求一个原来静止的镭核衰变时放出的能量．

Answer 1

分析：（1）由质数和核电荷数守恒写核反应方程；
（2）镭核衰变放出α粒子和氡核，分别在磁场中做匀速圆周运动，根据结合关系求出α粒子在磁场中做匀速圆周运动的半径，根据半径公式求出速度，求出α粒子的动能，衰变过程中动量守恒，求出氡核反冲的动能，两者动能之和即为原来静止的镭核衰变时放出的能量．

解答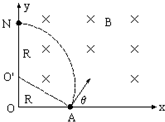：解：（1）镭核衰变方程为：

226 88

Ra→

222 86

Ra+

4 2

He
（2）镭核衰变放出α粒子和氡核，分别在磁场中做匀速圆周运动，α粒子射出y轴时平行于x轴，设α粒子在磁场中的轨道半径为R，其圆心位置如图d-1中O′点，有
(l-R)2+(

l

2

)2=R2，
则R=

5

8

l  
α粒子在磁场中做匀速圆周运动，有Bqv=m

v2

R

，即mv=BqR，
α粒子的动能为E1=

1

2

mv2=

(mv)2

2m

=

(5qBl)2

128m

       
∴衰变过程中动量守恒mv=m₀v₀，
则氡核反冲的动能为E2=

1

2

m0v02=

mE1

m0

 
∴E=E1+E2=

(5qBl)2(m+m0)

128mm0

   
答：（1）镭核的衰变方程为

226 88

Ra→

222 86

Ra+

4 2

He；
（2）一个原来静止的镭核衰变时放出的能量为

(5qBl)2(m+m0)

128mm0

．

点评：本题考查了核反应方程，和动量守恒定律，关键是知道谁和谁动量守恒及粒子在匀强磁场中的运动情况．