题目内容
3.两颗行星的质量分别为m1和m2,它们绕太阳运动的轨道半径为R1和R2、若m1=2m2、R1=4R2,则它们的周期之比T1:T2是多少?分析 根据开普勒第三定律得到行星的周期与轨道半径的关系式,再进行求解.
解答 解:根据开普勒第三定律$\frac{{R}^{3}}{{T}^{2}}$=k得:它们的周期之比为$\frac{{T}_{1}}{{T}_{2}}=\sqrt{\frac{{{R}_{1}}^{3}}{{{R}_{2}}^{3}}}=\frac{8}{1}$.
答:它们的周期之比T1:T2是8:1.
点评 解决本题的关键要掌握开普勒第三定律,熟练运用比例法求解.也可以根据万有引力等于向心力列式解答.

练习册系列答案
相关题目
13.关于万有引力公式F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,以下说法正确的是( )
| A. | 公式只适用于星球之间的引力计算,不适用于质量较小的物体 | |
| B. | 当两物体间的距离趋近于0时,万有引力趋近于无穷大 | |
| C. | 两物体间的万有引力也符合牛顿第三定律 | |
| D. | 公式适用于两质点;也适用于两个质量分布均匀的球体,r应取两球心间的距离 |
14.牛顿以天体之间普遍存在着引力为依据,运用严密的逻辑推理,建立了万有引力定律.在牛顿创建万有引力定律的过程中,以下说法错误的是( )
| A. | 接受了胡克等科学家关于“吸引力与两中心距离的平方成反比”的猜想 | |
| B. | 根据地球上一切物体都以相同加速度下落的事实,得出物体受地球的引力与其质量成正比,即F∝m的结论 | |
| C. | 根据F∝m和牛顿第三定律,分析了地、月间的引力关系,进而得出F∝m1、m2 | |
| D. | 根据大量实验数据得出了比例系数G的大小 |
11.下列说法中正确的是( )
| A. | 居里夫人首先发现了天然放射现象 | |
| B. | 对天然放射现象的研究建立了原子的核式结构 | |
| C. | 压力和温度对放射性元素衰变的快慢没有任何影响 | |
| D. | 贝克勒耳通过对天然放射现象的研究,发现了质子和中子 |
18. 如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧保持竖直),下列关于能的叙述正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧保持竖直),下列关于能的叙述正确的是( )
 如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧保持竖直),下列关于能的叙述正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧保持竖直),下列关于能的叙述正确的是( )| A. | 弹簧的弹性势能不断增大 | |
| B. | 小球的动能先增大后减小 | |
| C. | 小球的重力势能先增大后减小 | |
| D. | 小球的弹性势能和重力势能总和先增大后减小 |
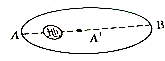 如图所示,一人造卫星绕地球作椭圆轨道运动,试比较该卫星在近地点与远地点时的重势能大小.
如图所示,一人造卫星绕地球作椭圆轨道运动,试比较该卫星在近地点与远地点时的重势能大小.